COMP7801 Topic 4 Top-k

Background #

Multidimensional Data #

• Flat relational tables
• Multimedia feature vectors
• Data warehouse data
• Spatial data
• Text documents

Attribute Types #

• Attributes of multidimensional tuples may have variable types
  • Ordinal (e.g., age, salary)
  • Nominal categorical values (e.g., color, religion)
  • Binary (e.g., gender, owns_property)
• Basic queries: range, NN, similarity

Basic Queries #

• (Range) selection query
  • Returns the records that qualify a (multidimensional) range predicate
  • Example:
    • Return the employees of age between 45 and 50 and salary above $100,000
• Distance (similarity) query
  • Returns the records that are within a distance from a reference record.
  • Example:
    • Find images with feature vectors of Euclidean distance at most ε with the feature vector of a given image
• Nearest neighbor (similarity) query
  • Replaces distance bound by ranking predicate

Top-k Search Methods #

• Rank aggregation
• Index-based methods

Top-k Query #

• Given a set of objects (e.g., relational tuples),
• Returns the k objects with the highest combined score, based on an aggregate function f.
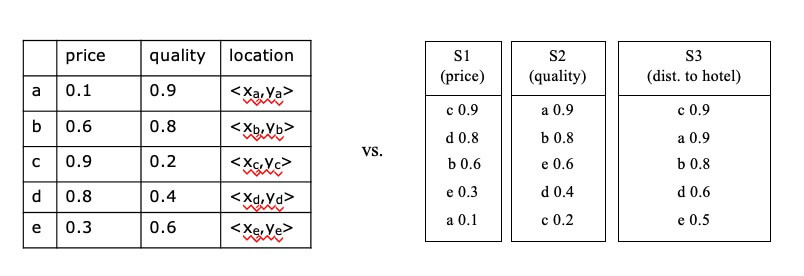
• Example:
  • Relational table containing information about restaurants, with attributes(e.g. price, quality, location)
  • f: sum(-price, quality, -dist(location,my_hotel))‏
  • attribute value ranges are usually normalized
    • E.g., all values in a (0,1) range
    • otherwise some attribute may be favored in f

Top-k Query Variants #

• Apply on single table, or ranked lists of tuples ordered by individual attributes

• Ranked inputs in the same or different servers (centralized or distributed data)

• Standalone query or operator in a more complex query plan

• Incremental retrieval of objects with highest scores (k is not predefined)

• Top-k joins

SELECT h.id, s.id
FROM House h School s
WHERE h.location=s.location
ORDER BY h.price + 10 ∗ s.tuition
LIMIT 5

• Probabilistic/approximate top-k retrieval

• Random and/or sorted accesses at ranked inputs

Top-k Query Evaluation #

• Most solutions assume distributive, monotone aggregate functions (e.g. f=sum)

  • distributive: f(x,y,z,w)= f(f(x,y),f(z,w))
    • e.g., A+B+C+D = (A+B) + (C+D)
  • monotone: if x<y and z<w, then f(x,z)<f(y,w)

• Solutions based on 1-D ordering and merging sorted lists (rank aggregation)

• Solutions based on multidimensional indexing

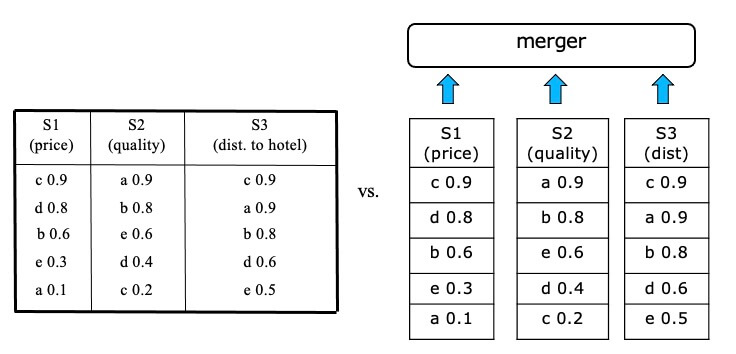
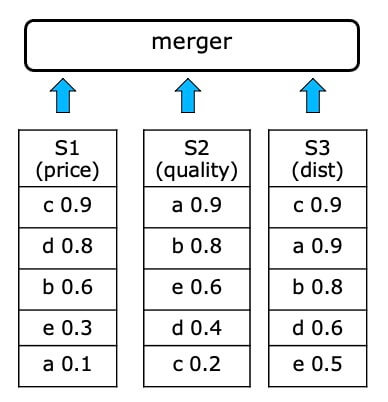
Rank Aggregation #

• Solutions based on 1-D ordering and merging sorted lists (rank aggregation)
• Assume that there is a total ranking of theobjects for each attribute that can be used in top-k queries
• These sorted inputs can be accessed sequentially and/or by random accesses

Advantages and Drawbacks #

• Advantages：
  • can be applied on any subset of inputs (arbitrary subspace)
  • appropriate for distributed data
  • appropriate for top-k joins
  • easy to understand and implement
• Drawbacks:
  • slower than index-based methods
  • require inputs to be sorted

TA: Threshold Algorithm #

Introduction #

• Iteratively retrieves objects and their atomic scores from the ranked inputs in a round-robin fashion.
• For each encountered object x, perform random accesses to the inputs where x has not been seen.
• Maintain top-k objects seen so far.
• T = f($l_1$, . . . , $l_m$) is the score derived when applying the aggregation function to the last atomic scores seen at each input. If the score of the k-th object is no smaller than T, terminate.

Example of TA(k=1,f=sum) #

• STEP 1
  • top-1 is c, with score 2.0
  • T=sum(0.9,0.9,0.9)=2.7
  • T>top-1, we proceed to another round of accesses

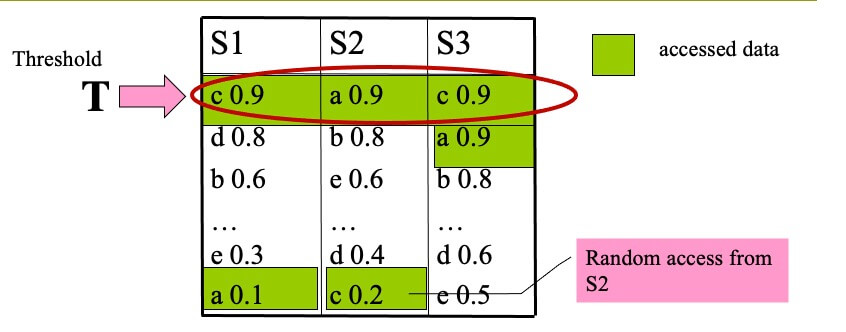
• STEP 2
  • top-1 is b, with score 2.2
  • T=sum(0.8,0.8,0.9)=2.5
  • T>top-1, we proceed to another round of accesses

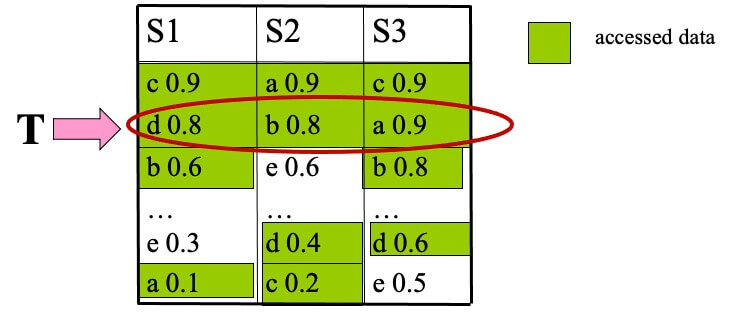
• STEP 3
  • top-1 is b, with score 2.2
  • T=sum(0.6,0.6,0.8)=2.0
  • T≤top-1, terminate and output (b,2.2)

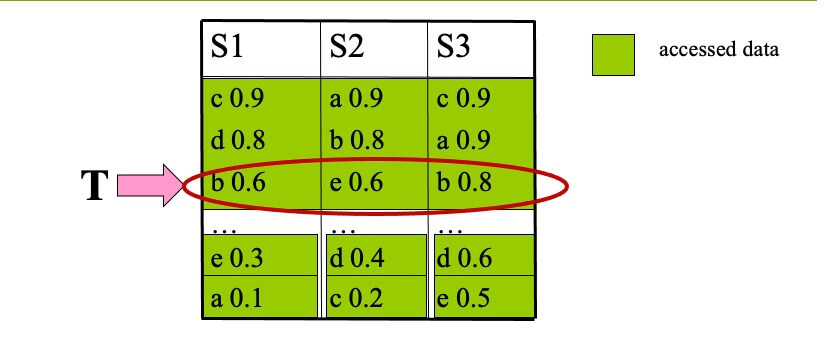
Properties of TA #

• Used as a standard module for merging ranked lists in many applications
• Usually finds the result quickly
• Depends on random accesses, which can be expensive
• random accesses are impossible in some cases
  • e.g., an API allows to access objects incrementally by ranking score, but does not provide the score of a given object

NRA: No Random Accesses #

Introduction #

• Iteratively retrieves objects and their atomic scores from the ranked inputs in a round-robin fashion.
• For each object x seen so far at any input maintain:
  • f_x_ub: upper bound for x’s aggregate score (f_x)
  • f_x_lb: lower bound for x’s aggregate score (f_x)
• W_k = k objects with the largest f^lb.
• If the smallest f^lb in W_k is at least the largest f_x_ub of any object x not in W_k, then terminate and report W_k as top-k result.

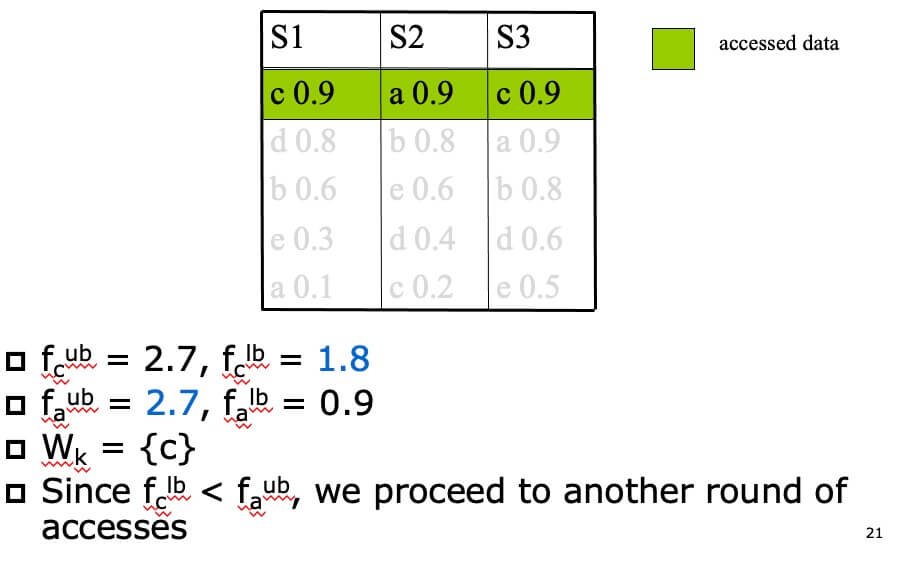
Example of NRA(k=1,f=sum) #

• STEP 1

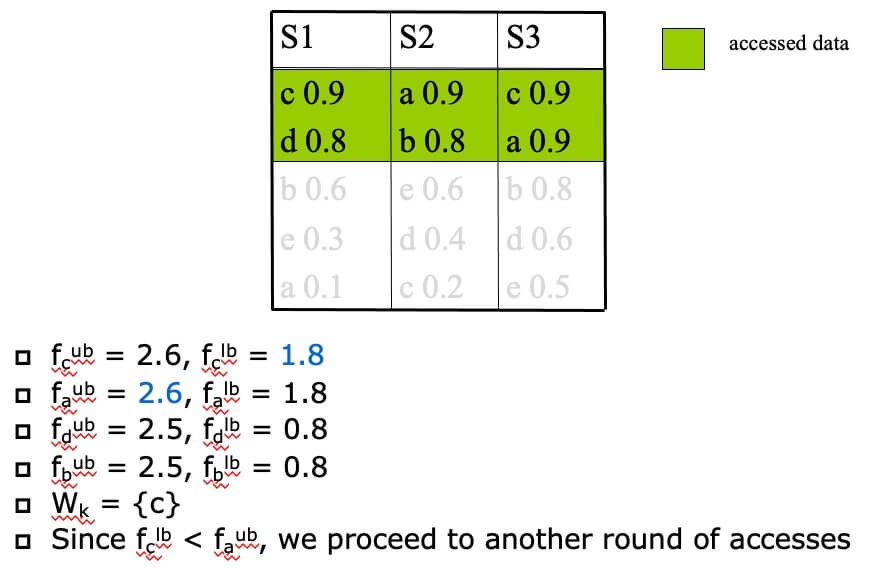
• STEP 2

• STEP 3

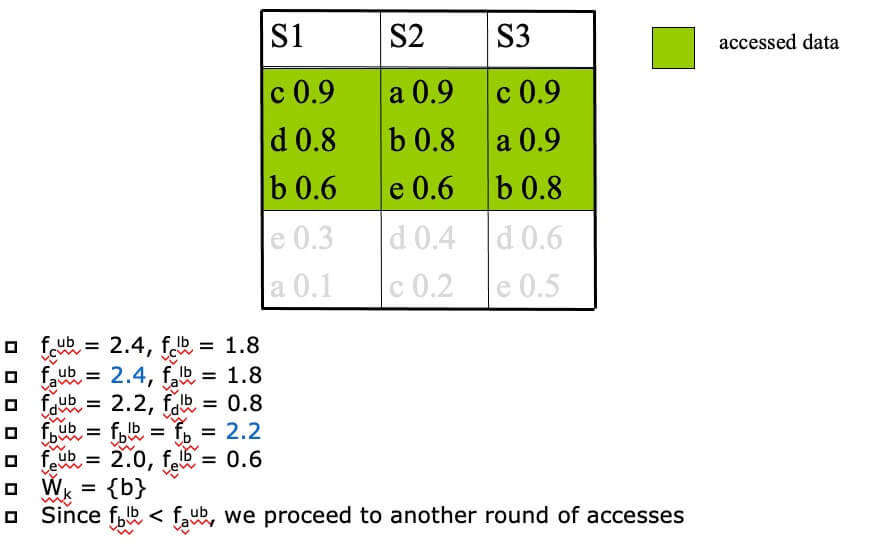
• STEP 4

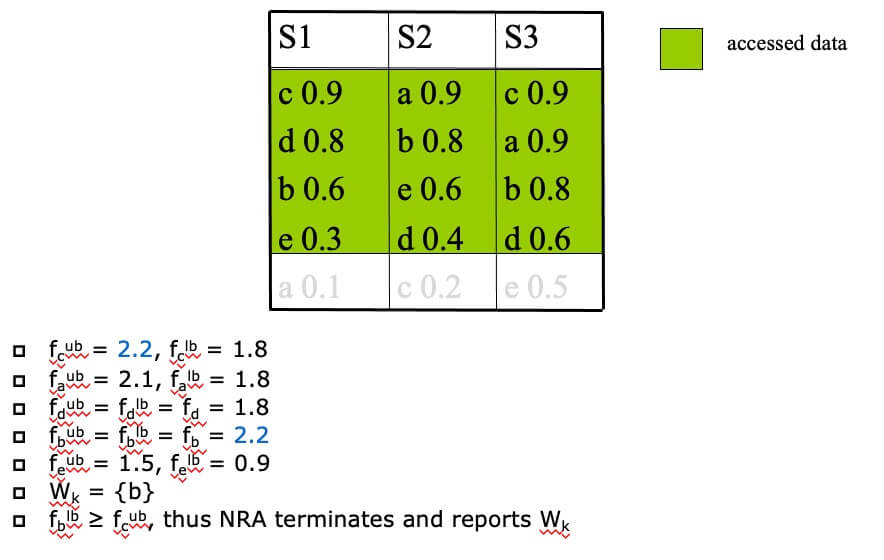
NRA Properties #

• More generic than TA, since it does not depend on random accesses
• Can be cheaper than TA, if random accesses are very expensive
• NRA accesses objects sequentially from all inputs and updates the upper bounds for all objects seen so far unconditionally.
  • Cost: O(n) per access (the expected distinct number of objects accessed so far is O(n))
  • No input list is pruned until the algorithm terminates

LARA: LAttice-based Rank Aggregation #

• LARA: An efficient NRA implementation
• Based on 3 observations about the top-k candidates
• Operates differently in the two (growing, shrinking) phases
• Takes its name from the lattice used in the shrinking phase
• Extendable to various top-k query variants