COMP7404 Computational Intelligence and Machine Learning

Topic 3 Adversarial Search

A Multi-agent Competitive Environment

• Other agents are planning against us
• Goals are in conflict (not necessarily)

Game Definition

• A game can be defined as
  • s : States
  • s0: Initial state
  • Player(s) : Defines which player has the move
  • Actions(s) : Returns a set of legal moves
  • Result(s,a) : Defines the result of a move
  • TerminalTest(s) : True when game is over, false otherwise
  • Utility(s,p) : Defines the final numeric value for a game that ends in terminal state s for player p
• A game tree can be constructed
  • Nodes are game states and edges are moves

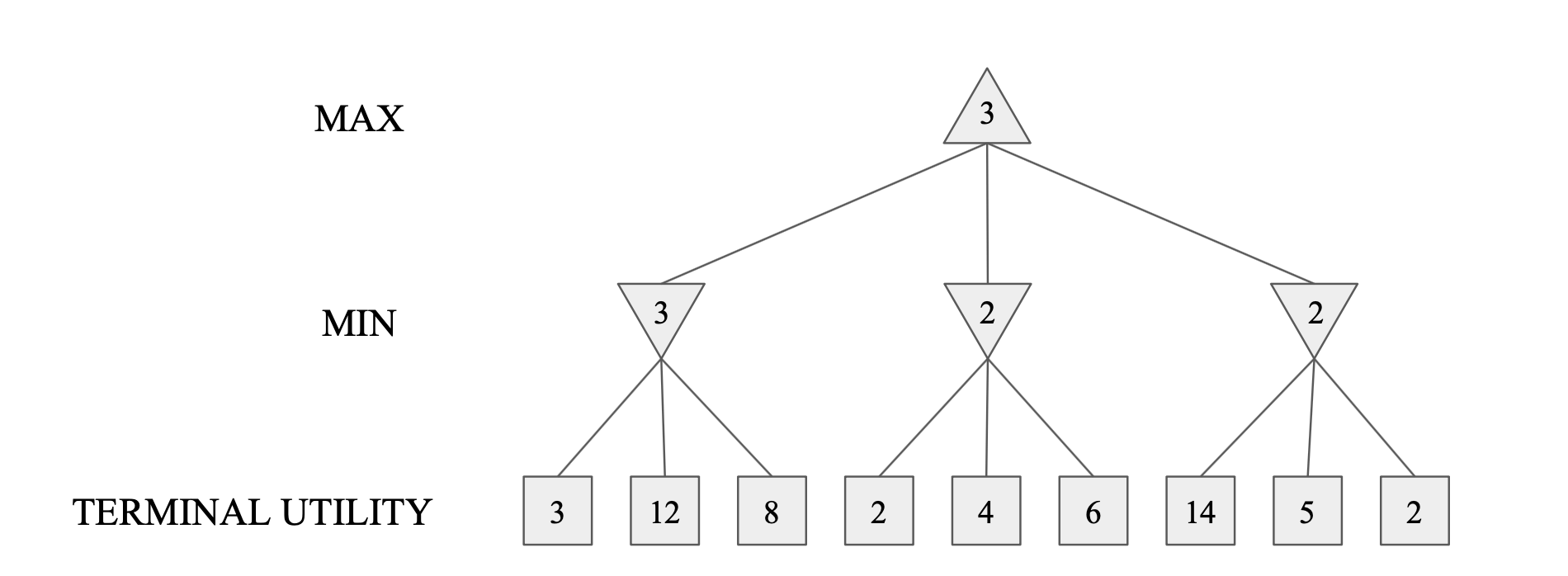
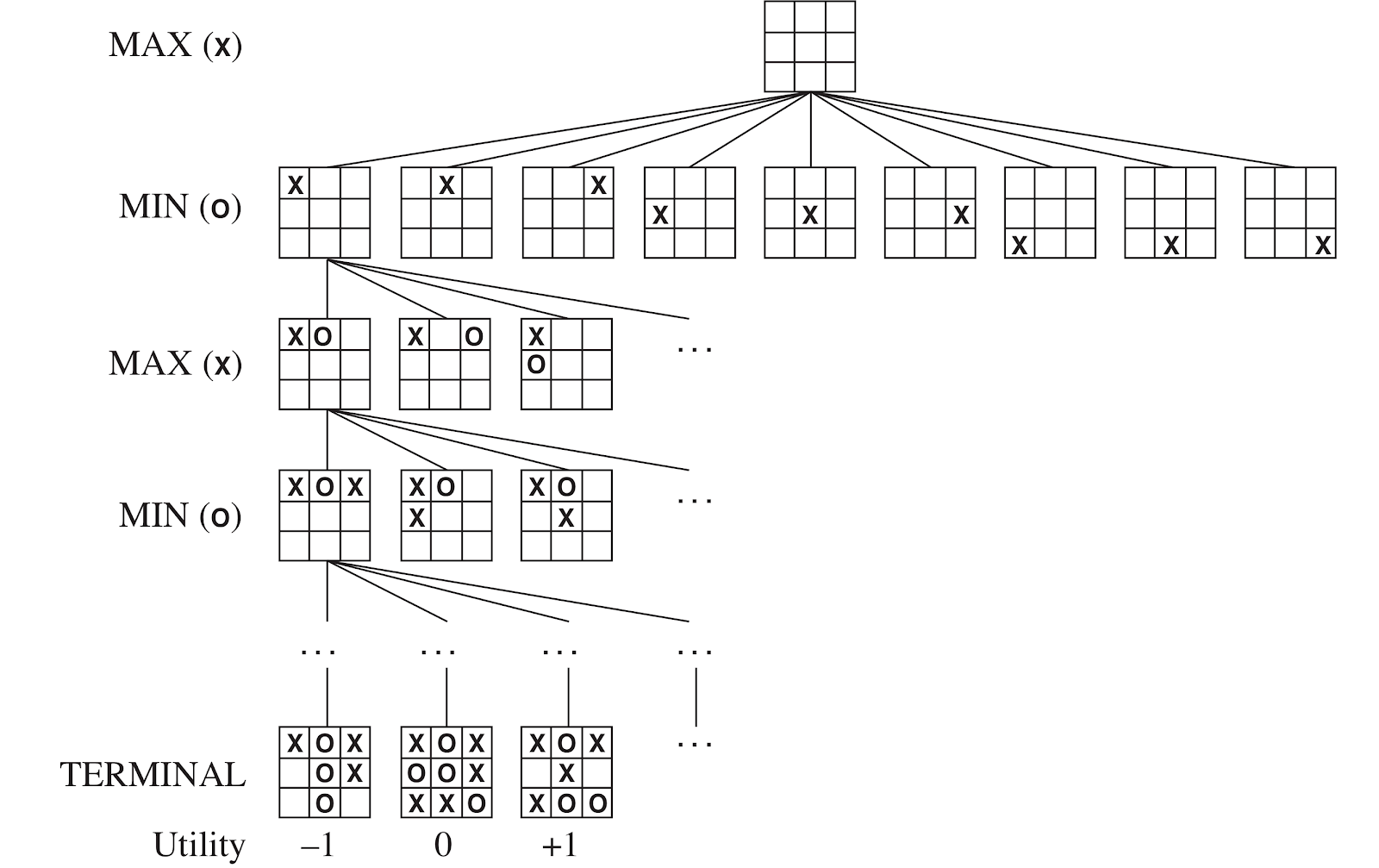
Tic-Tac-Toe Game Tree

Minimax Search

• A state-space search tree
• Players alternate turns
• Compute each node’s minimax value
  • the best achievable utility against a rational (optimal) adversary
  • 
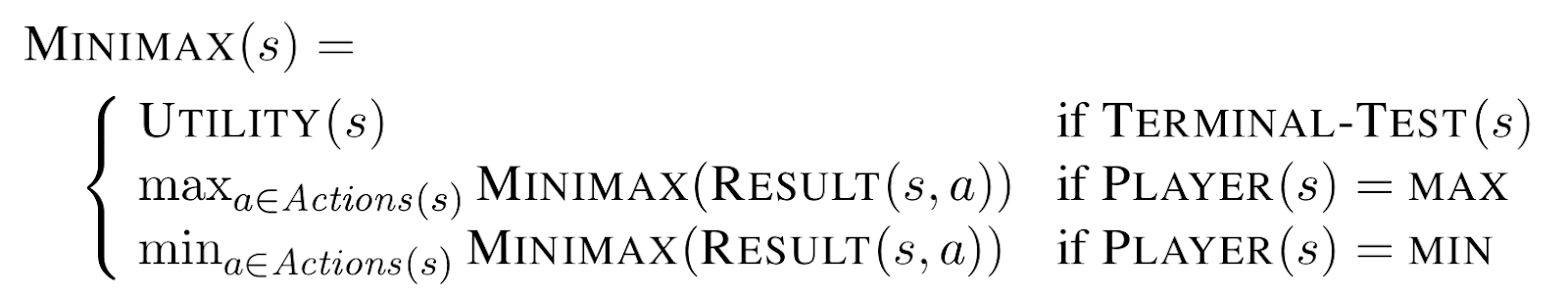
• Will lead to optimal strategy
  • Best achievable payoff against best play
• Example
  • 
• Implementation
  • 
• Properties
  • Complete - Yes, if tree is finite
  • Optimal - In general no, yes against an optimal opponent
  • Time complexity - O(b^m)
  • Space complexity - O(bm)

Depth-Limit Search (DLS)

• A depth limit search (DLS)
  • Search only to a limited depth in the tree
  • Replace terminal utilities with an evaluation function for non-terminal positions
• Problems
  • Guarantee of optimal play is gone
  • Need to design evaluation function
• An evaluation function
  • An evaluation function Eval(s) scores non-terminals in depth-limited search
    • An estimate of the expected utility of the game from a given position
  • Ideal function
    • The actual minimax value of the position
  • The performance of a game-playing program depends strongly on the quality of its evaluation functio

𝛼-𝛽 Pruning Algorithm

• Min version
  • Consider Min’s value at some node n
  • n will decrease (or stay constant) while the descendants of n are examined
  • Let m be the best value that Max can get at any choice point along the current path from the root
  • If n becomes worse (<) than m
    • Max will avoid it
    • Stop considering n’s other children
• Max version is symmetric
• Properties
  • Pruning has no effect on the minimax value at the root
  • Values of intermediate nodes might be wrong
    • Action selection not appropriate for this simple version of alpha-beta pruning
• Move ordering
  • The effectiveness of alpha-beta pruning is highly dependent on the order in which states are examined
  • It is worthwhile to try to examine first the successors that are likely best
    • Examine only O(b^(m/2)) nodes to pick the best move, instead of O(bm) for minimax

A Reference Note

Expectimax Search

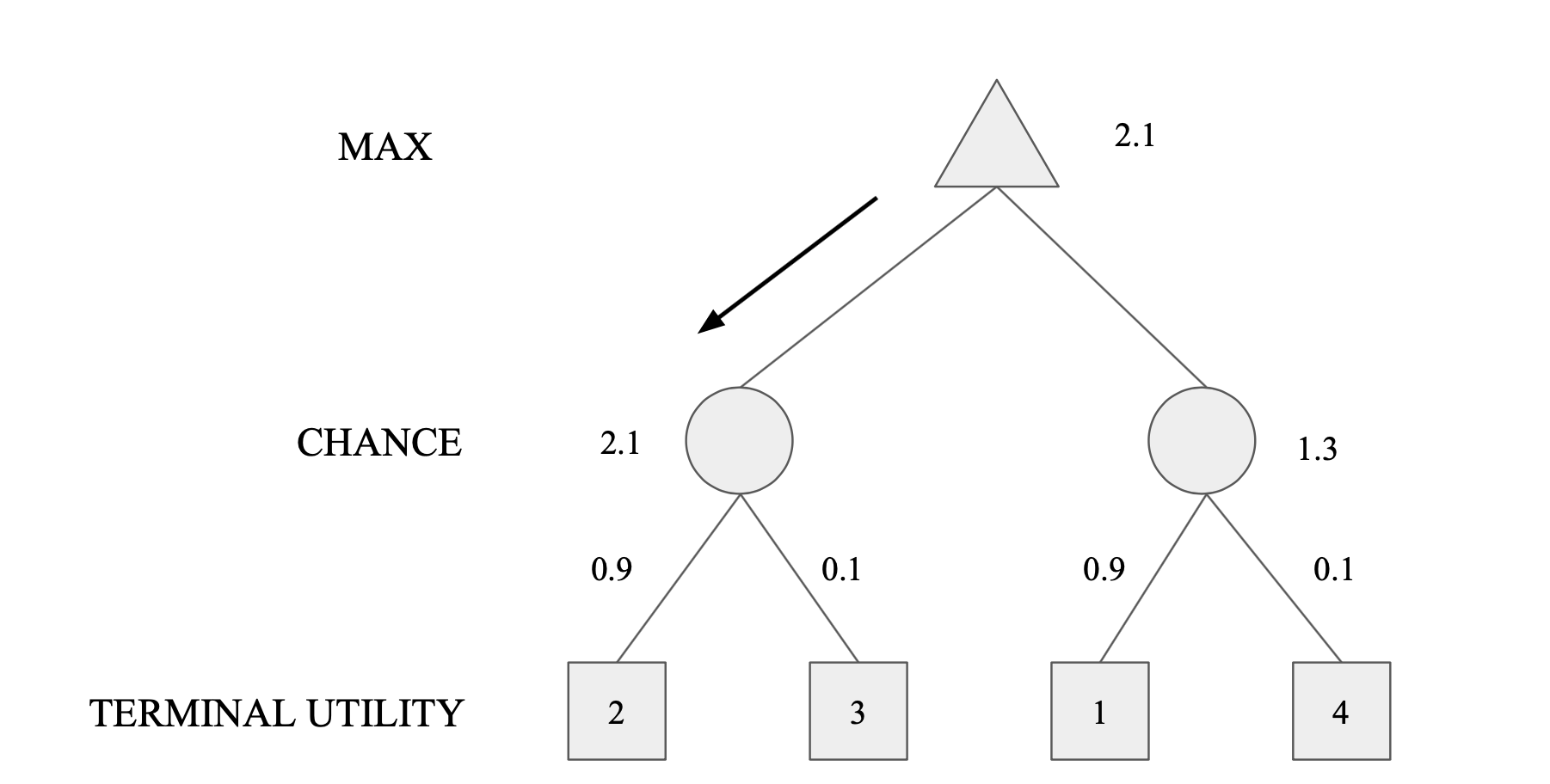
• Values reflect average case outcomes, not worst case outcomes
• Expectimax search computes the expected score under optimal play
  • Max nodes as in minimax search
  • Chance nodes are like min nodes but the outcome is uncertain
  • Calculate their expected utilities
    • i.e., take weighted average of children
• Expectiminimax
  • Environment is an extra “random agent” player that moves after each min/max agent

Multi-Agent Utilities

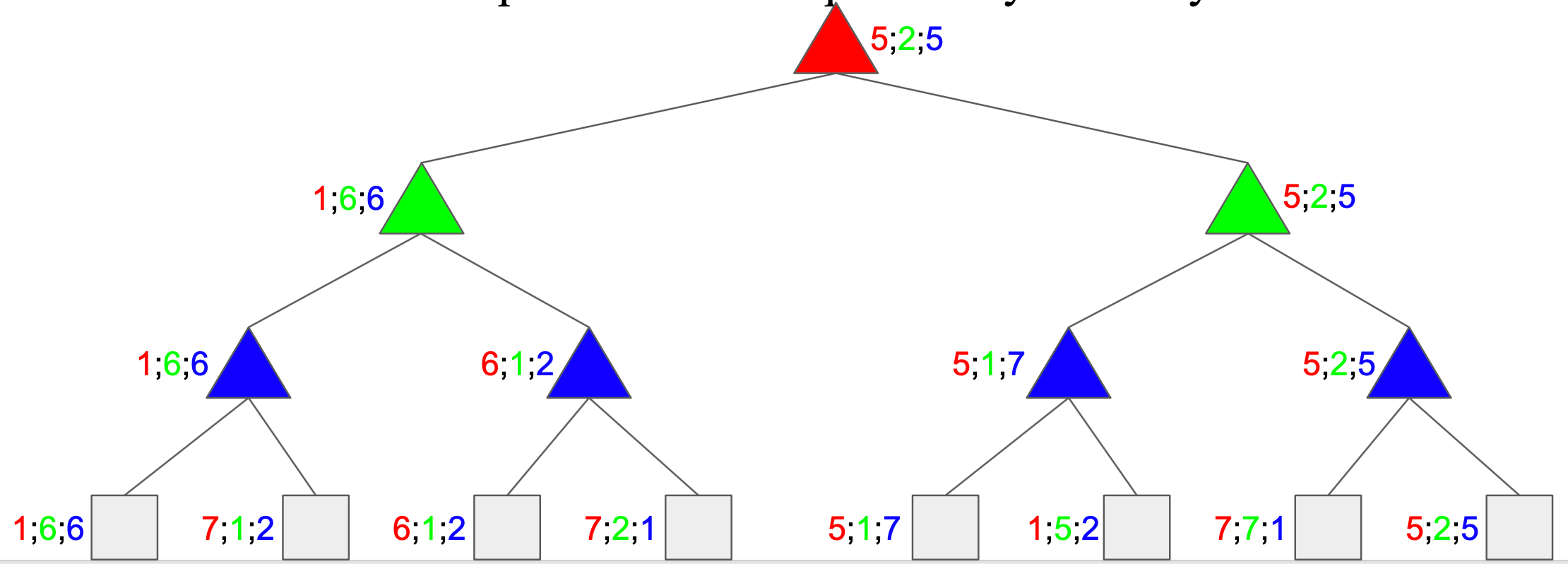
• Generalisation of minimax
  • Terminals and nodes have utility vectors
  • Each player maximizes its own component
  • Gives rise to cooperation and competition dynamically

1. A Reference Note1
2. A Reference Note2