COMP7103 Data Mining #
Topic 3 Clustering #
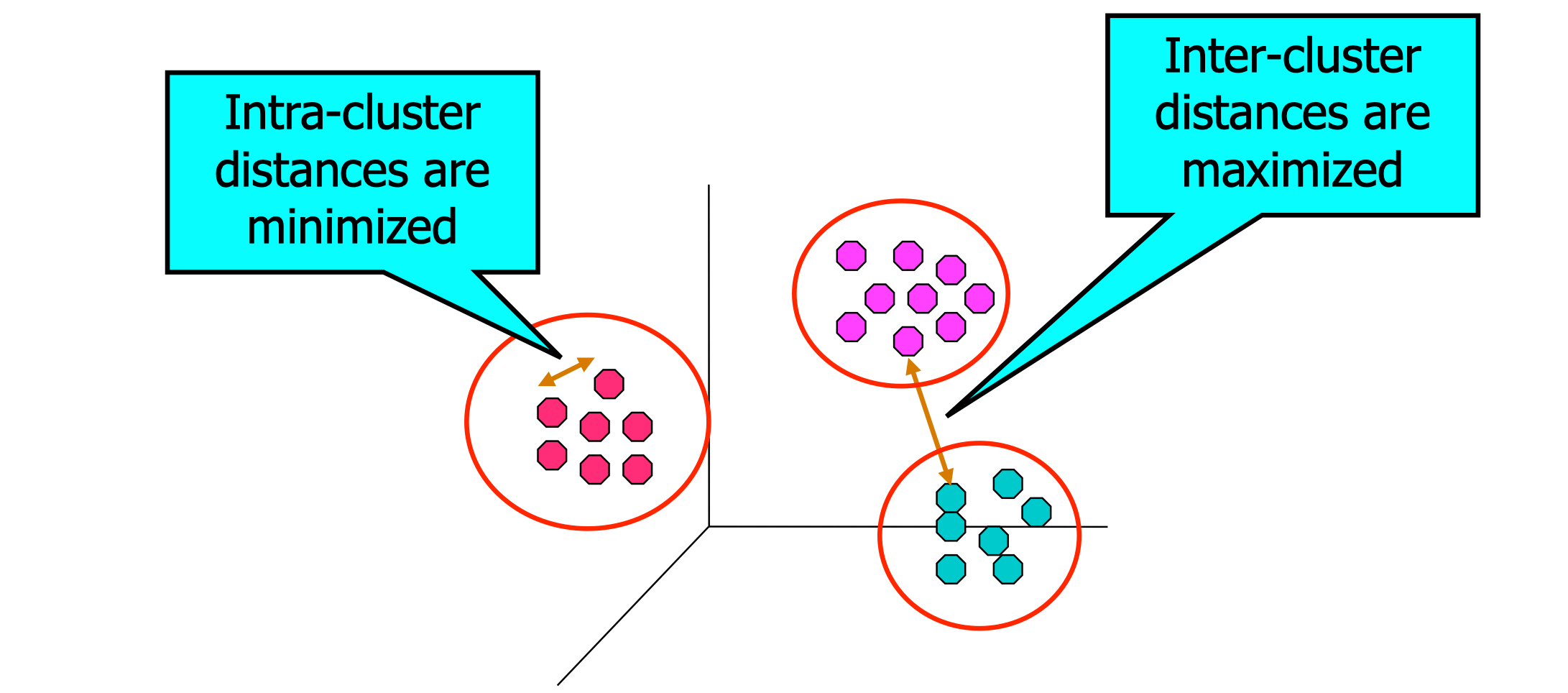
Cluster Analysis #
Finding groups of objects such that the objects in a group will be similar (or related) to one another and different from (or unrelated to) the objects in other groups
Application #
- Understanding
- Group related documents for browsing, group genes and proteins that have similar functionality, or group stocks with similar price fluctuations
- Summarization
- Reduce size of large data sets
Types of Clusterings #
- Partitional Clustering
- A division data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset
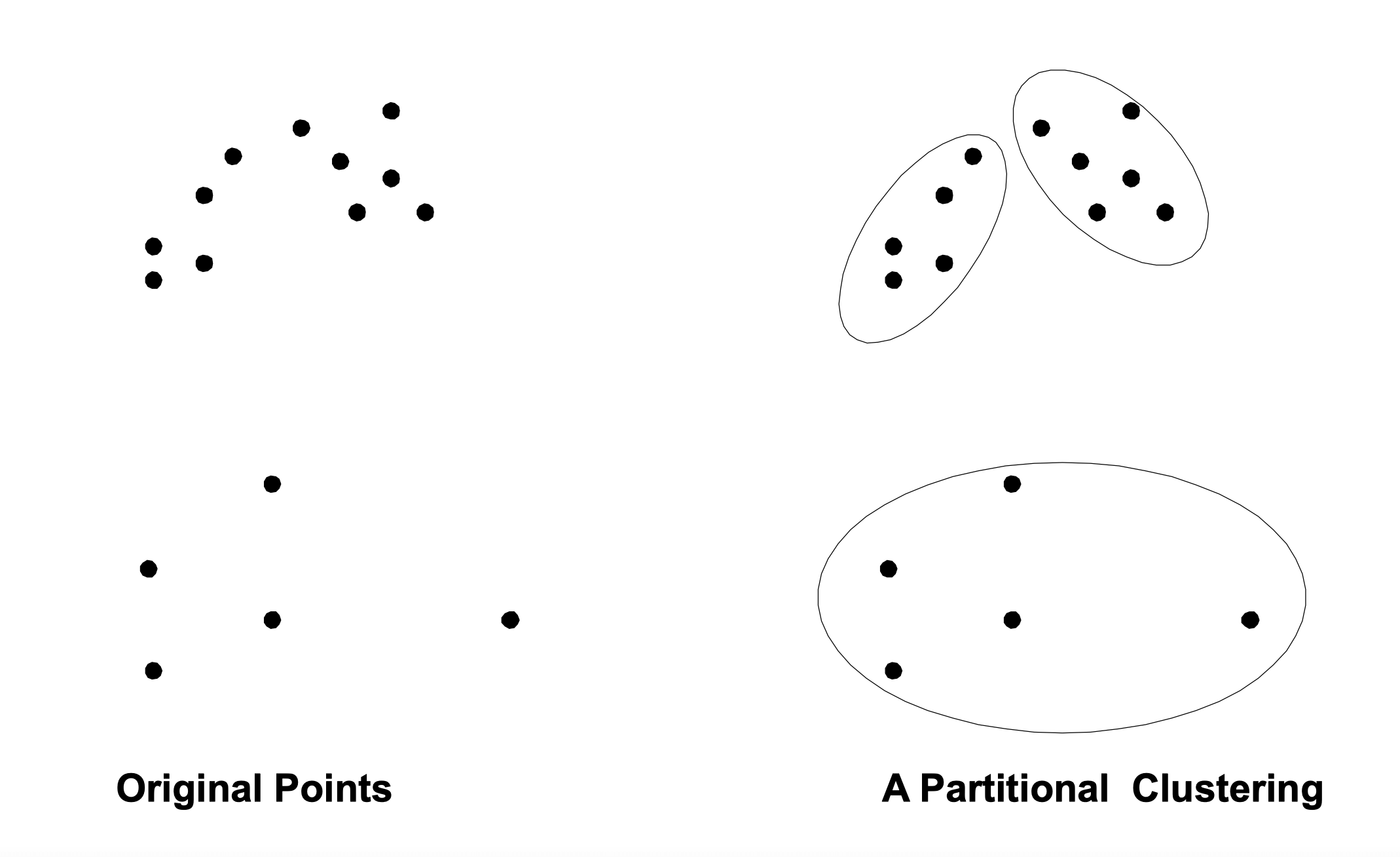
- A division data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset
- Hierarchical clustering
- A set of nested clusters organized as a hierarchical tree
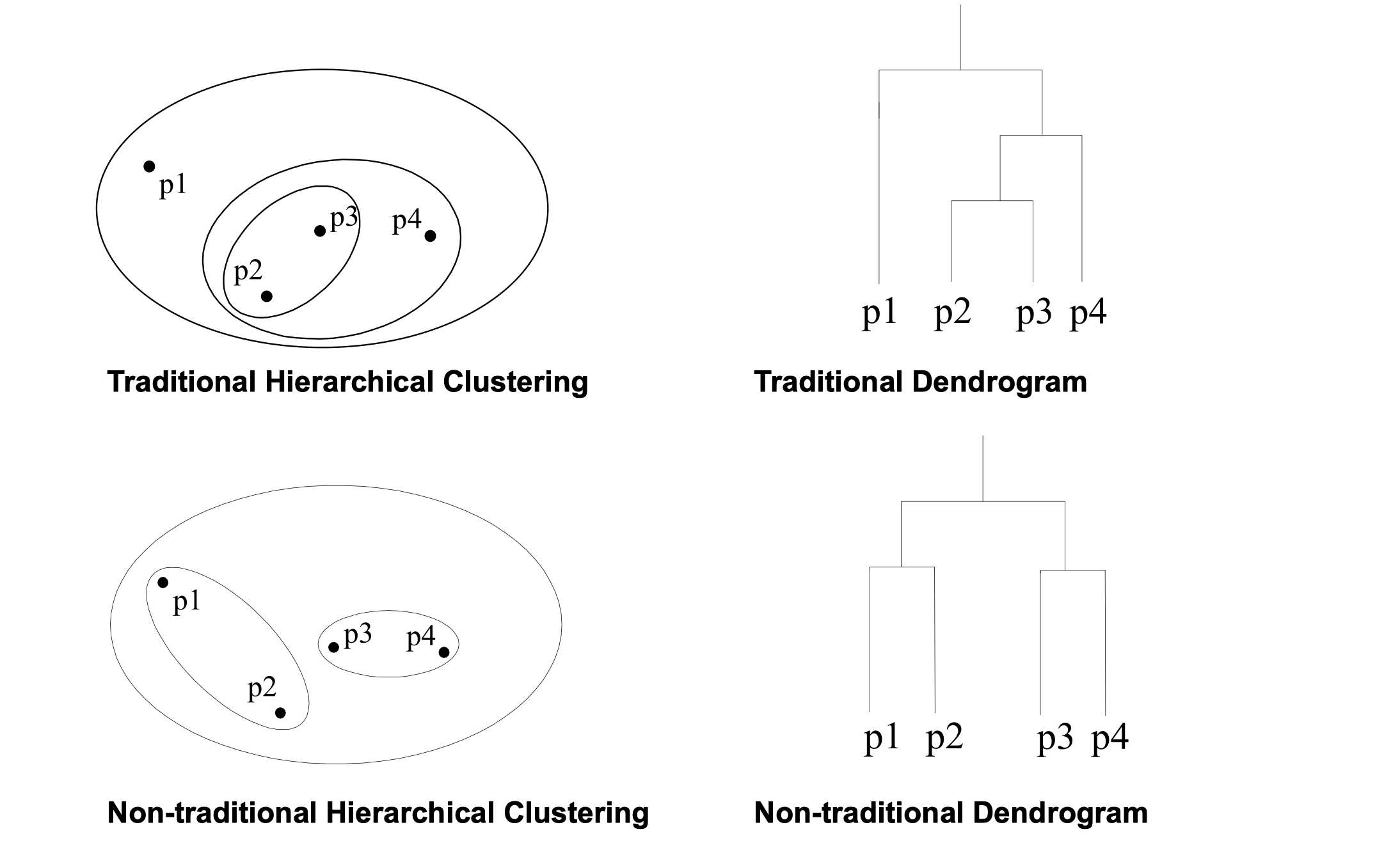
- A set of nested clusters organized as a hierarchical tree
- Other Distinctions Between Sets of Clusters
- Exclusive versus non-exclusive
- In non-exclusive clusterings, points may belong to multiple clusters
- Can represent multiple classes or 'border' points
- Fuzzy versus non-fuzzy
- In fuzzy clustering, a point belongs to every cluster with some weight between 0 and 1
- Weights must sum to 1
- Probabilistic clustering has similar characteristics
- Partial versus complete
- In some cases, we only want to cluster some of the data
- Heterogeneous versus homogeneous
- Cluster of widely different sizes, shapes, and densities
- Exclusive versus non-exclusive
Well-separated clusters #
A cluster is a set of points such that any point in a cluster is closer (or more similar) to every other point in the cluster than to any point not in the cluster

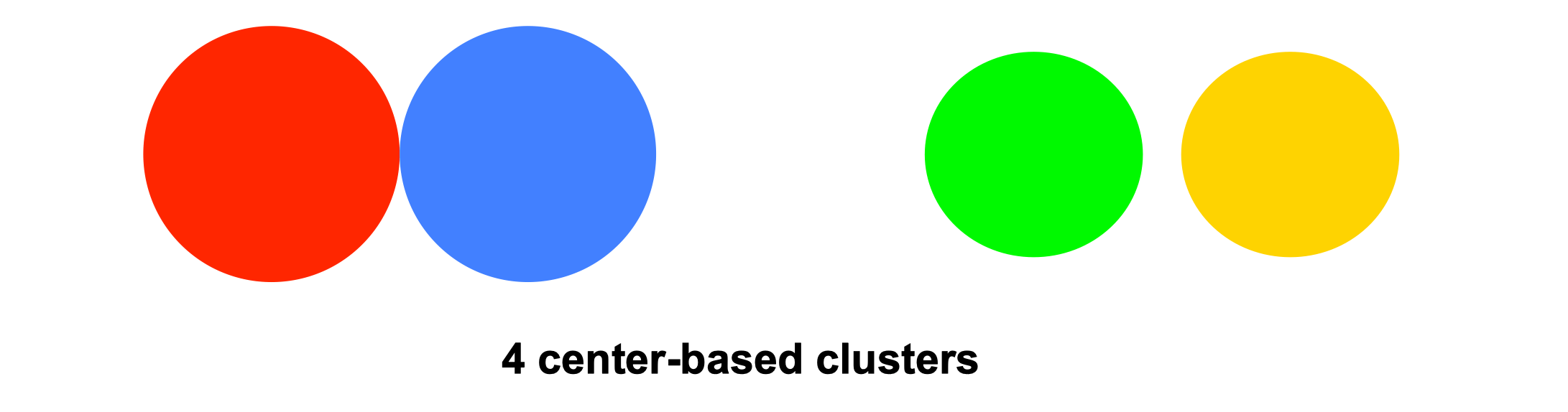
Center-based clusters #
A cluster is a set of objects such that an object in a cluster is closer (more similar) to the “center” of a cluster, than to the center of any other cluster
The center of a cluster is often a centroid, the average of all the points in the cluster, or a medoid, the most “representative” point of a cluster
Contiguity-Based clusters #
A cluster is a set of points such that a point in a cluster is closer (or more similar) to one or more other points in the cluster than to any point not in the cluster
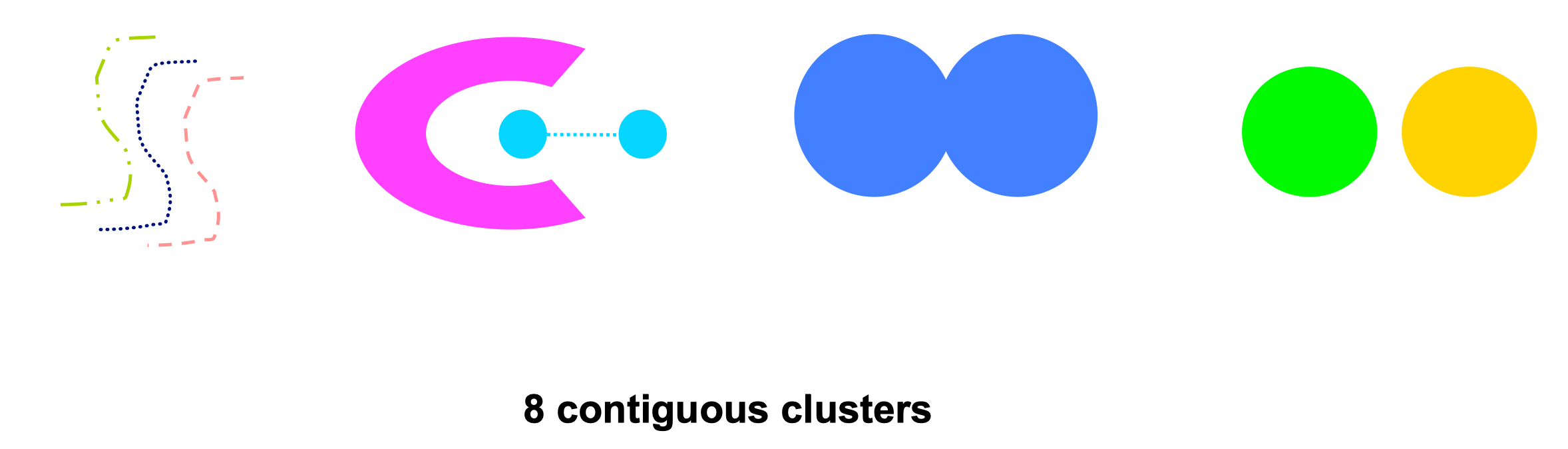
Density-based clusters #
A cluster is a dense region of points, which is separated by low-density regions, from other regions of high density
Used when the clusters are irregular or intertwined, and when noise and outliers are present

Conceptual Clusters #
Finds clusters that share some common property or represent a particular concept

K-means #
- Input
- integer k>0, set S of points in the euclidean space
- Output
- A (partitional) clustering of S
Step
- Select k points in S as the initial centroids
- Repeat until the centroids do not change
- Form k clusters by assigning points to the closest centroids
- For each cluster recompute its centroid
Feature
- Initial centroids are often chosen randomly
- Centroids are often the mean of the points in the cluster
- 'Closeness' is measured by Euclidean distance, cosine similarity, correlation, etc.
Importance of Choosing Initial Centroids #

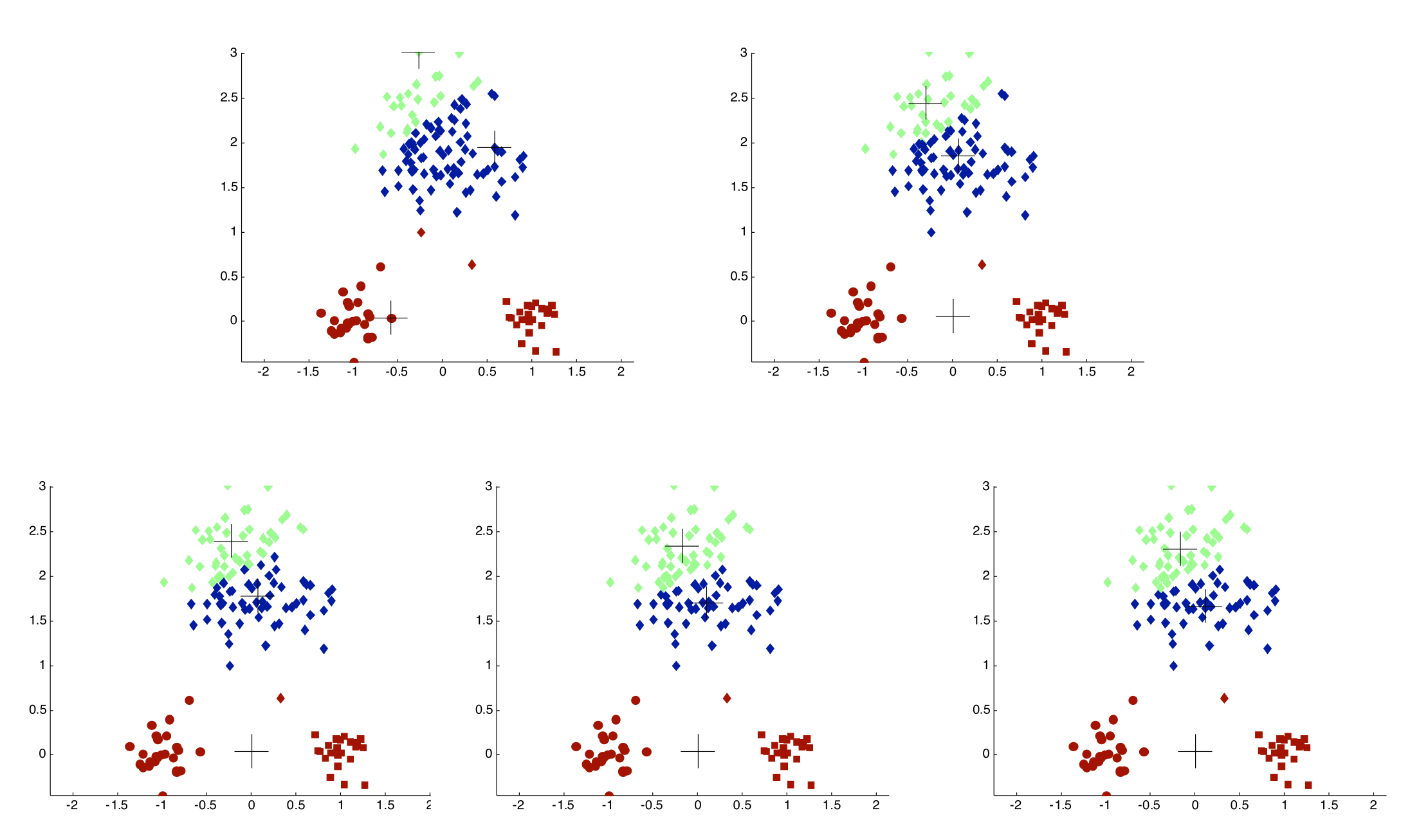
Evaluating K-means Clusterings #
- Most common measure is Sum of Squared Error (SSE)
- Given two clusterings, we can choose the one with smallest error
- Decreasing K might decrease SSE
- However, good clusterings with small K might have a lower SSE than poor clusterings with higher K
K-Means Always Terminates #
- Theorem
- K-means with Euclidean distance as distance always terminates
- Proof follows from the following lemmas
- We cannot obtain the same clustering more than once, otherwise we get the same SSE value
- Lemma 1
- The point y that minimizes the SSE in a cluster C is the mean of all points in C
- Lemma 2
- SSE strictly decreases.
- Lemma 3
- The total number of possible clusterings is finite (< n^k).
Solutions to Initial Centroids Problem #
- Multiple runs (helps but low success probability)
- Sample and use hierarchical clustering to determine initial centroids
- Select more than k initial centroids and then select among these initial centroids
- Postprocessing
- K-Means++
Handling Empty Clusters #
Basic K-means algorithm can yield less than k clusters (so called empty clusters)
- Pick the points that contributes most to SSE and move them to empty cluster
- Pick the points from the cluster with the highest SSE
- If there are several empty clusters, the above can be repeated several times
Updating Centers Incrementally #
- In the basic K-means algorithm, centroids are updated after all points are assigned to a centroid
- An alternative is to update the centroids after each assignment (incremental approach)
- More precisely, let C1 ,C2 ,…,C k be the current clusters. Reassign all points one by one to the best cluster. Let p in C i be the current point and suppose we re-assign it to Cj . Then, after that, recompute the centroid of C i and Cj
- Never get an empty cluster
- Introduces an order dependency
- More expensive
Pre-processing and Post-processing #
Pre-processing
- Normalize the data
- Eliminate outliers
Post-processing
- Eliminate small clusters that may represent outliers
- Split 'loose' clusters, i.e., clusters with relatively high SSE
- Merge clusters that are ‘close’ and that have relatively low SSE
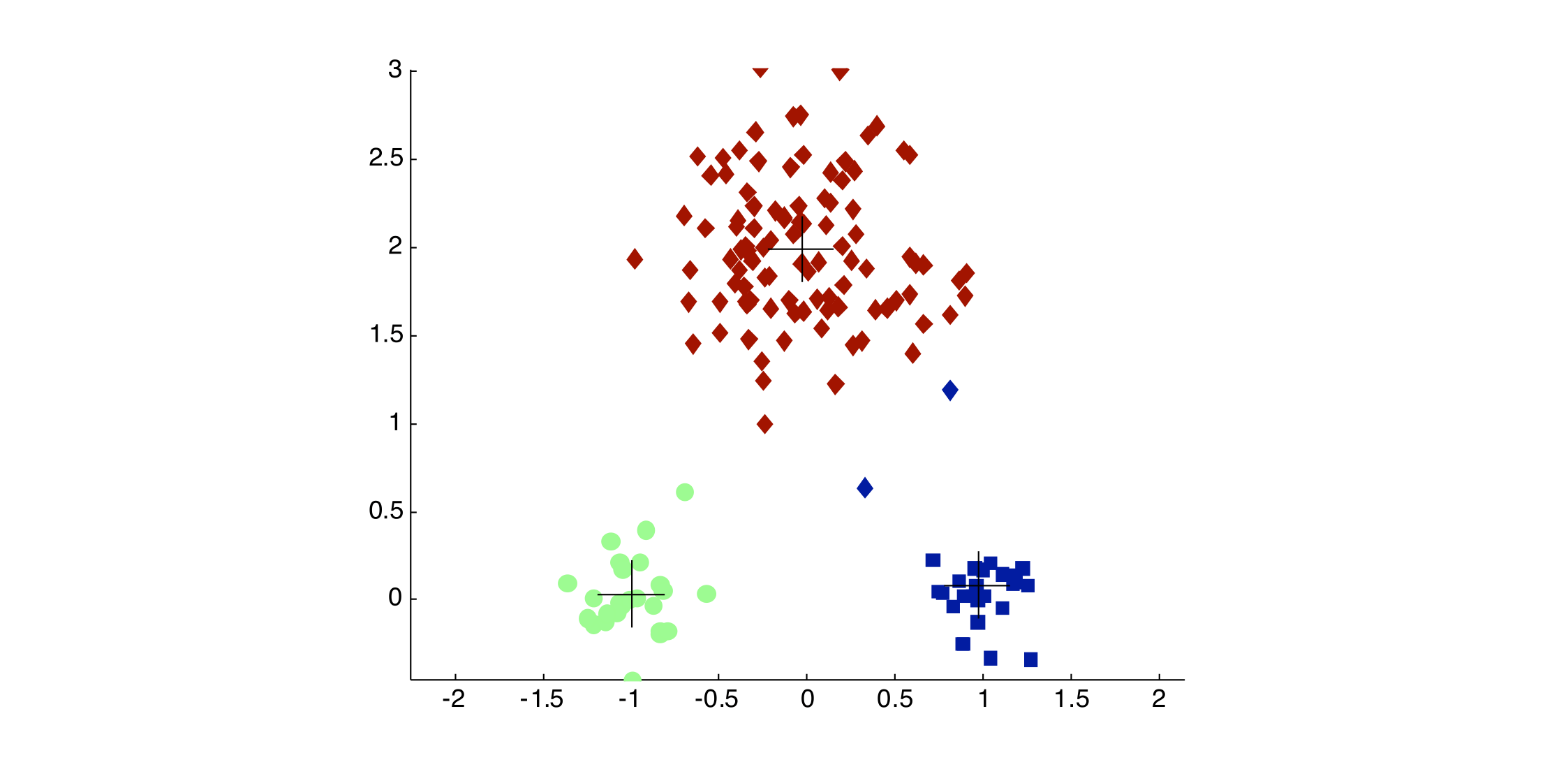
Limitations of K-means #
- K-means has problems when clusters are of differing
- Sizes
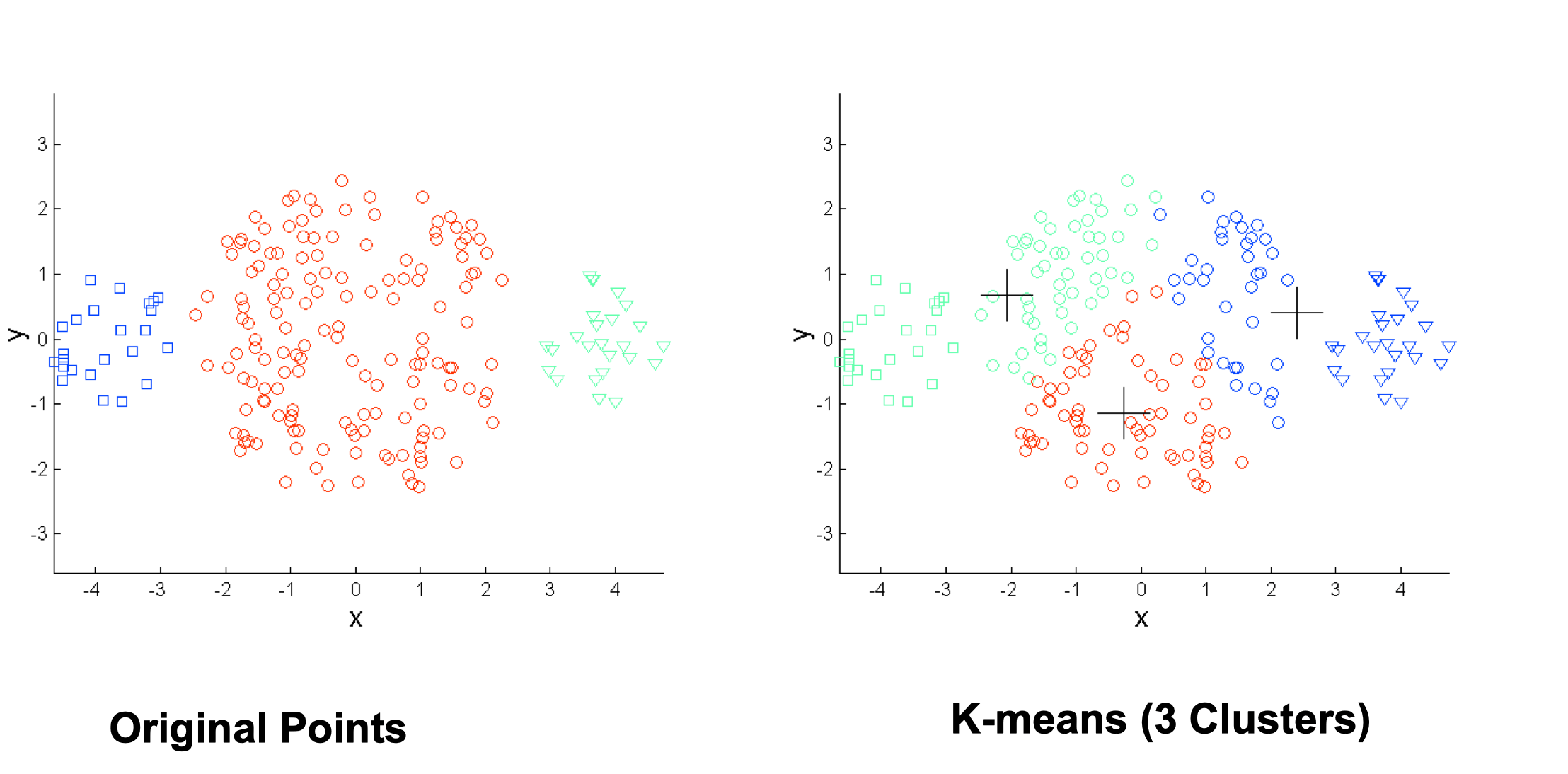
- Densities
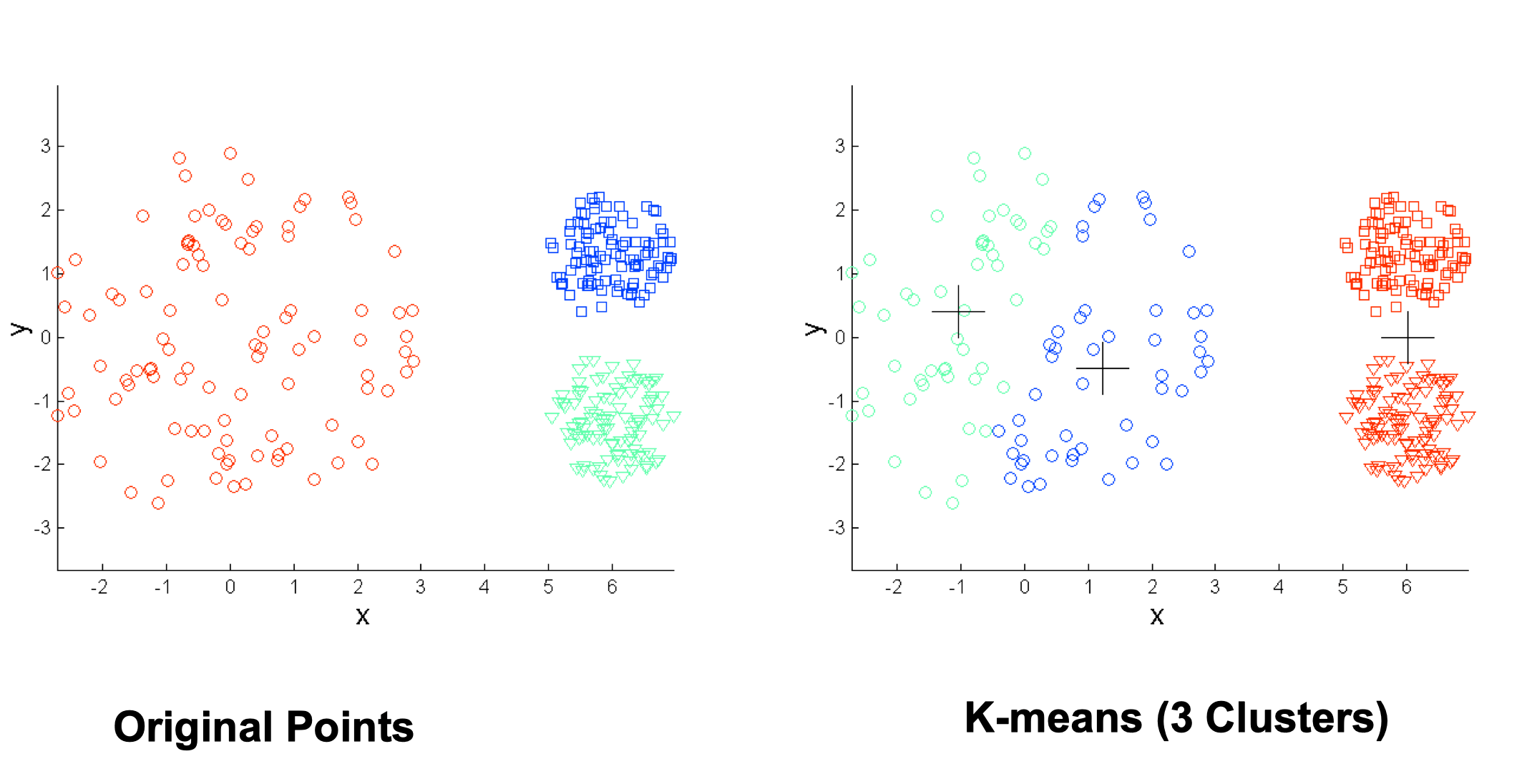
- Non-globular shapes
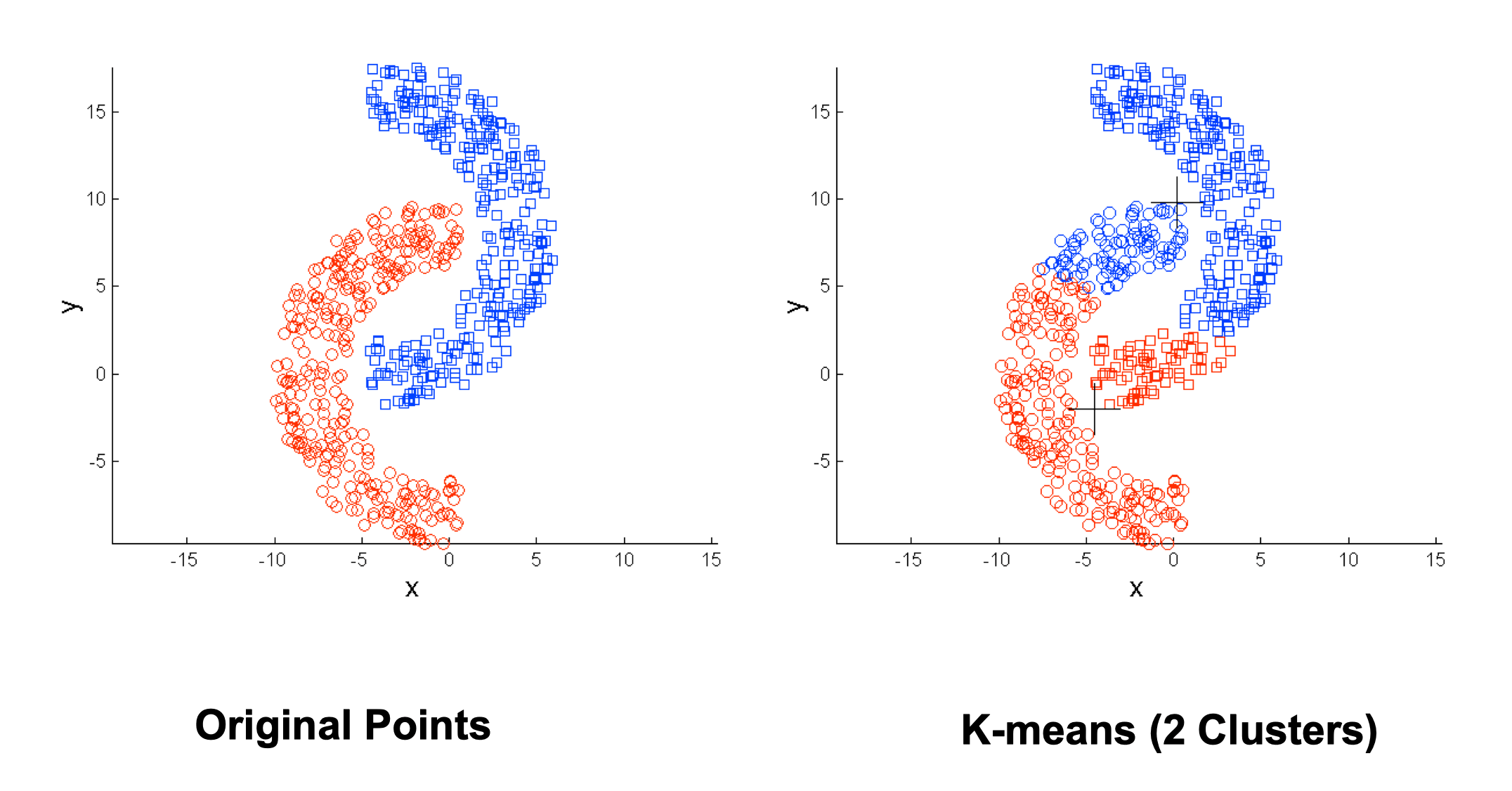
- Sizes
- K-means has problems when the data contains outliers
Overcoming K-means Limitations #
Use many clusters, find parts of clusters, but need to put together
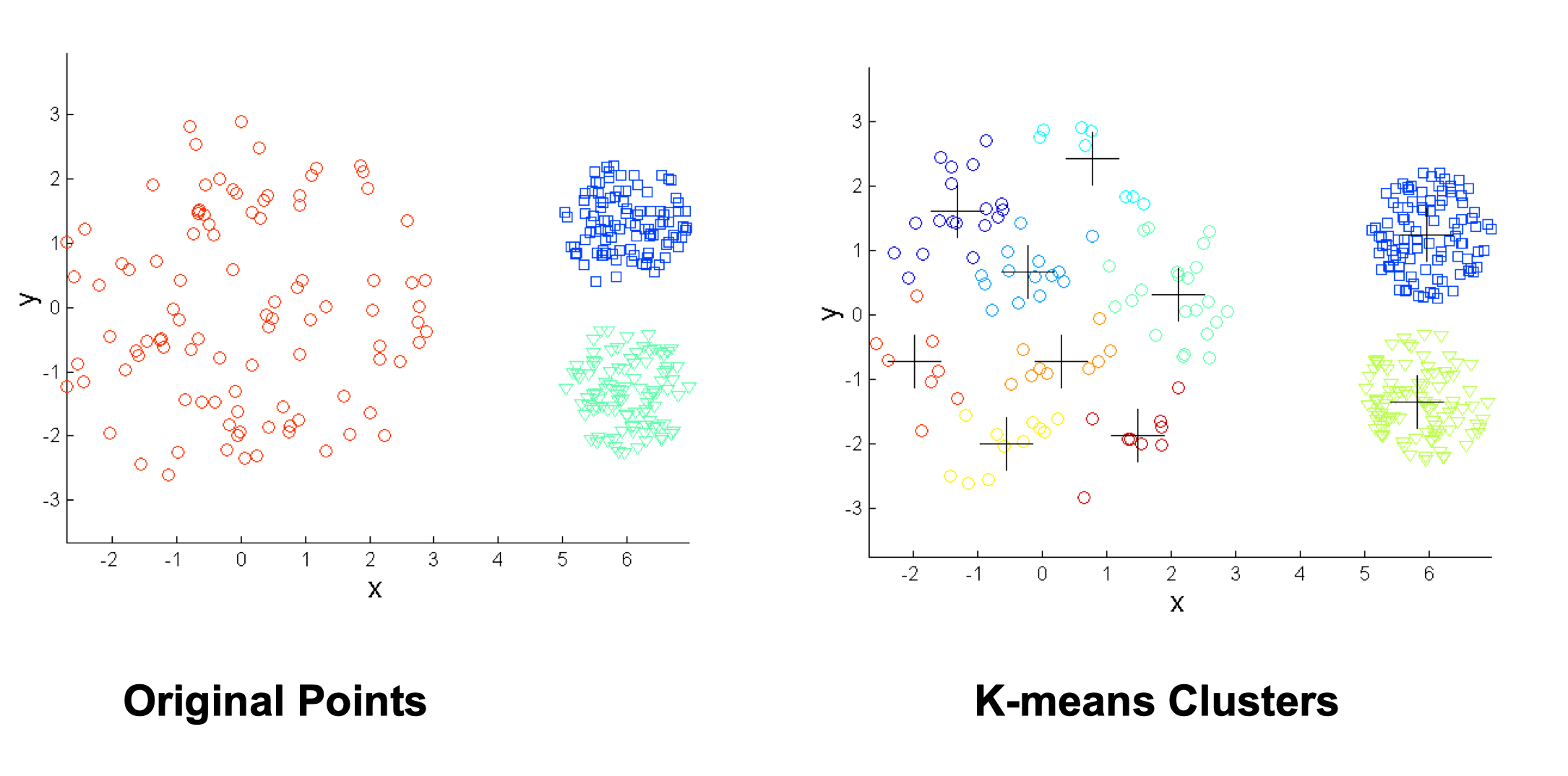
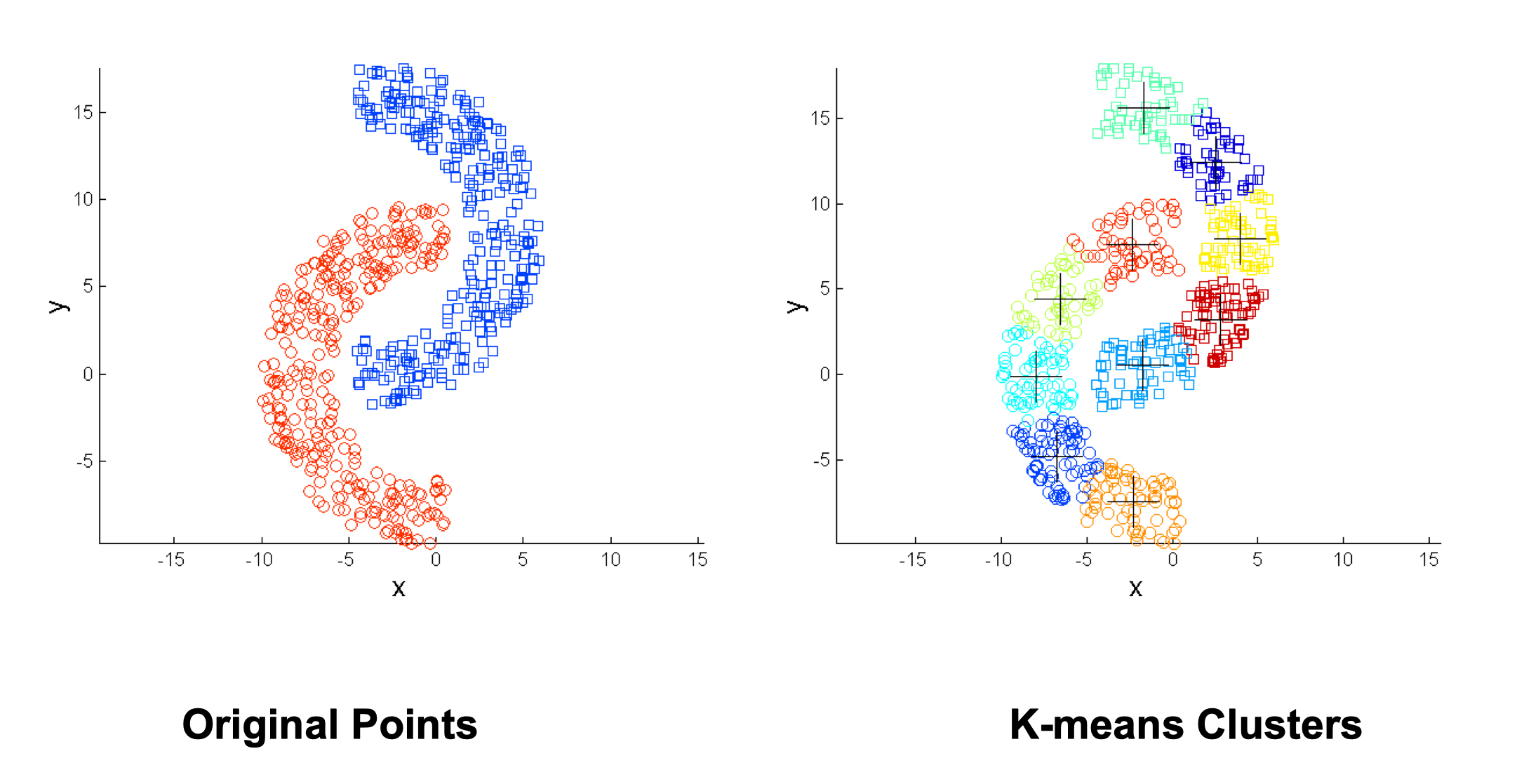
Hierarchical clustering #
- Produces a set of nested clusters organized as a hierarchical tree
- Can be visualized as a dendrogram
- A tree like diagram that records the sequences of merges or splits
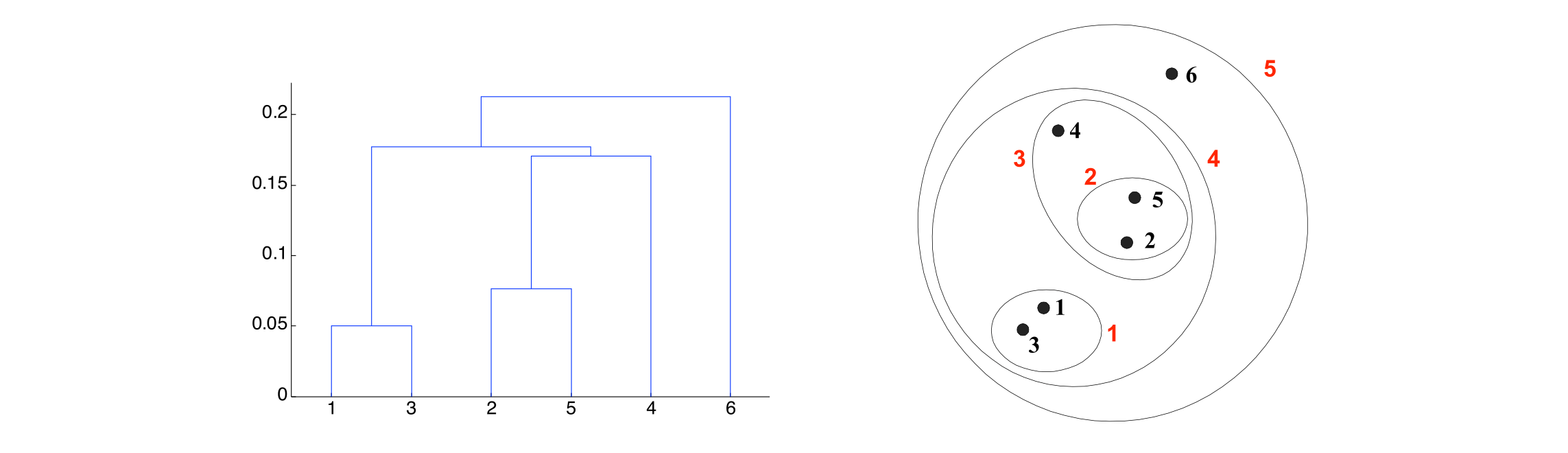
- A tree like diagram that records the sequences of merges or splits
Strengths of Hierarchical Clustering #
- Do not have to assume any particular number of clusters
- Any desired number of clusters can be obtained by ‘cutting’ the dendogram at the proper level
- They may correspond to meaningful taxonomies
- Example in biological sciences (e.g., animal kingdom, phylogeny reconstruction, …)
Two main types of hierarchical clustering #
- Agglomerative
- Start with the points as individual clusters
- At each step, merge the closest pair of clusters until only one cluster (or k clusters) left
- Divisive
- Start with one, all-inclusive cluster
- At each step, split a cluster until each cluster contains a point (or there are k clusters)
Traditional hierarchical algorithms use a similarity or distance matrix
- Merge or split one cluster at a time
Agglomerative Clustering Algorithm #
Most popular hierarchical clustering technique
- Let each data point be a cluster
- Compute the distance matrix n x n
- Repeat
- Merge the two closest clusters
- Update distance matrix
- Until only a single cluster remains
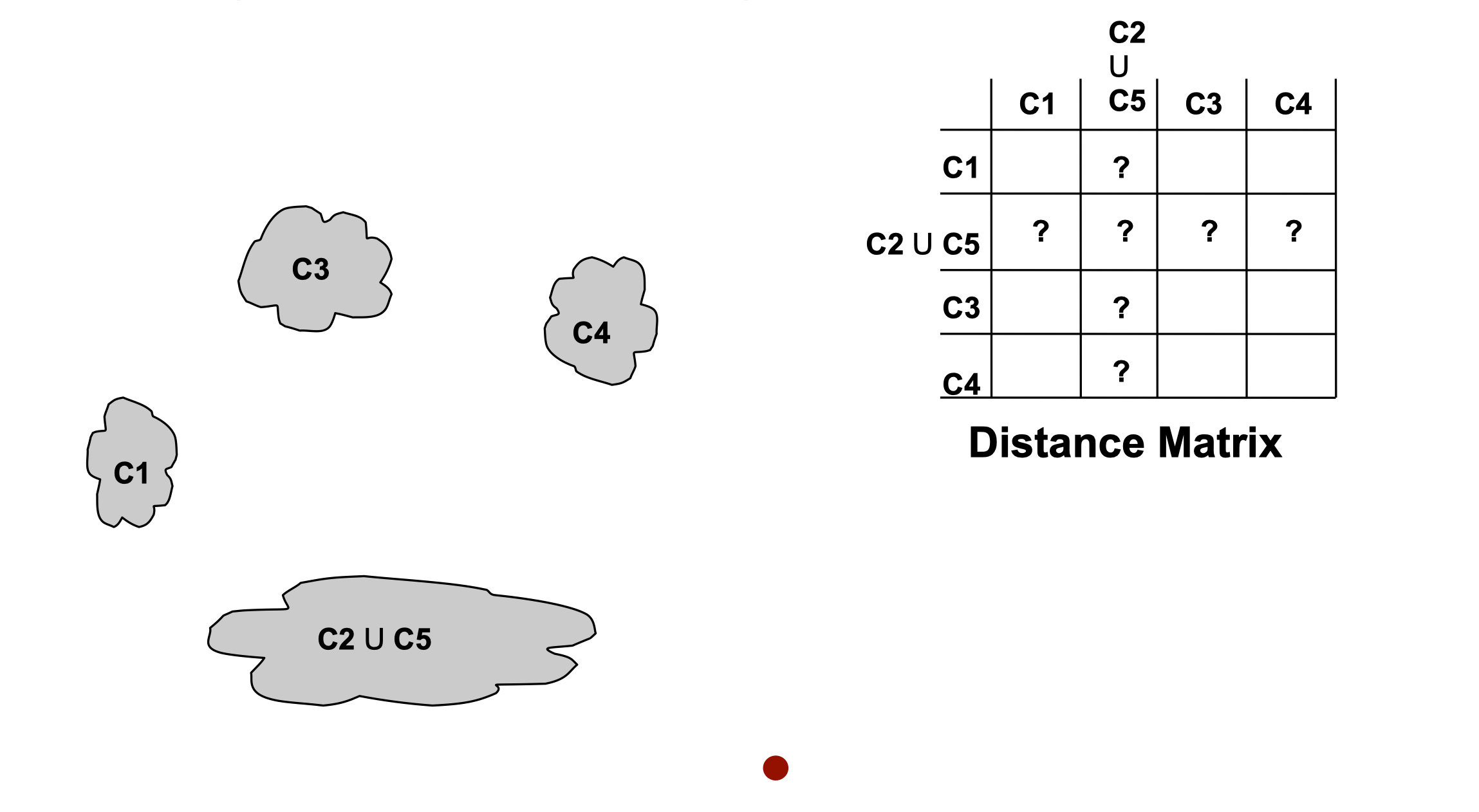
Procedure
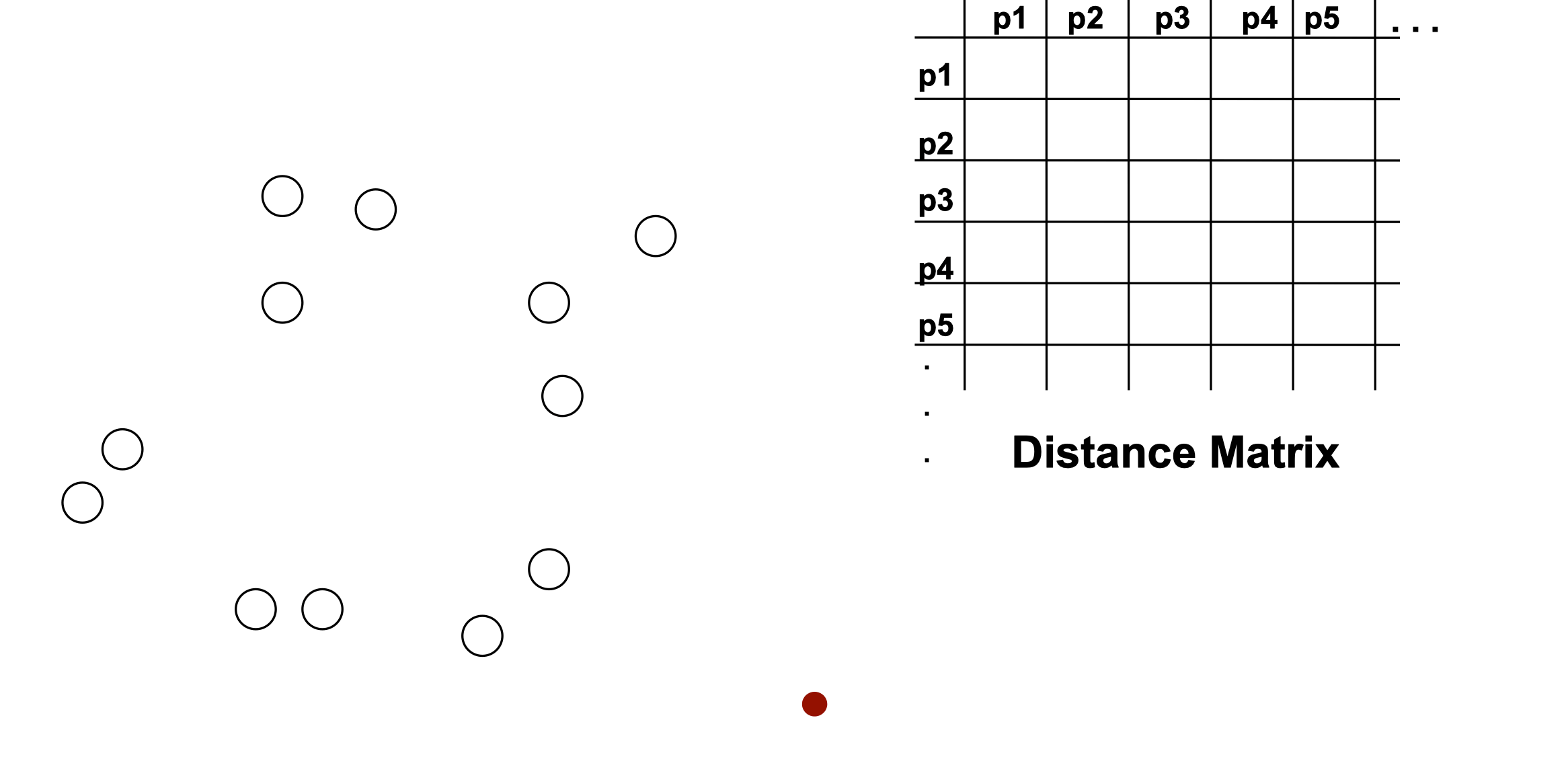
- Start with clusters of individual points and a distance matrix n x n
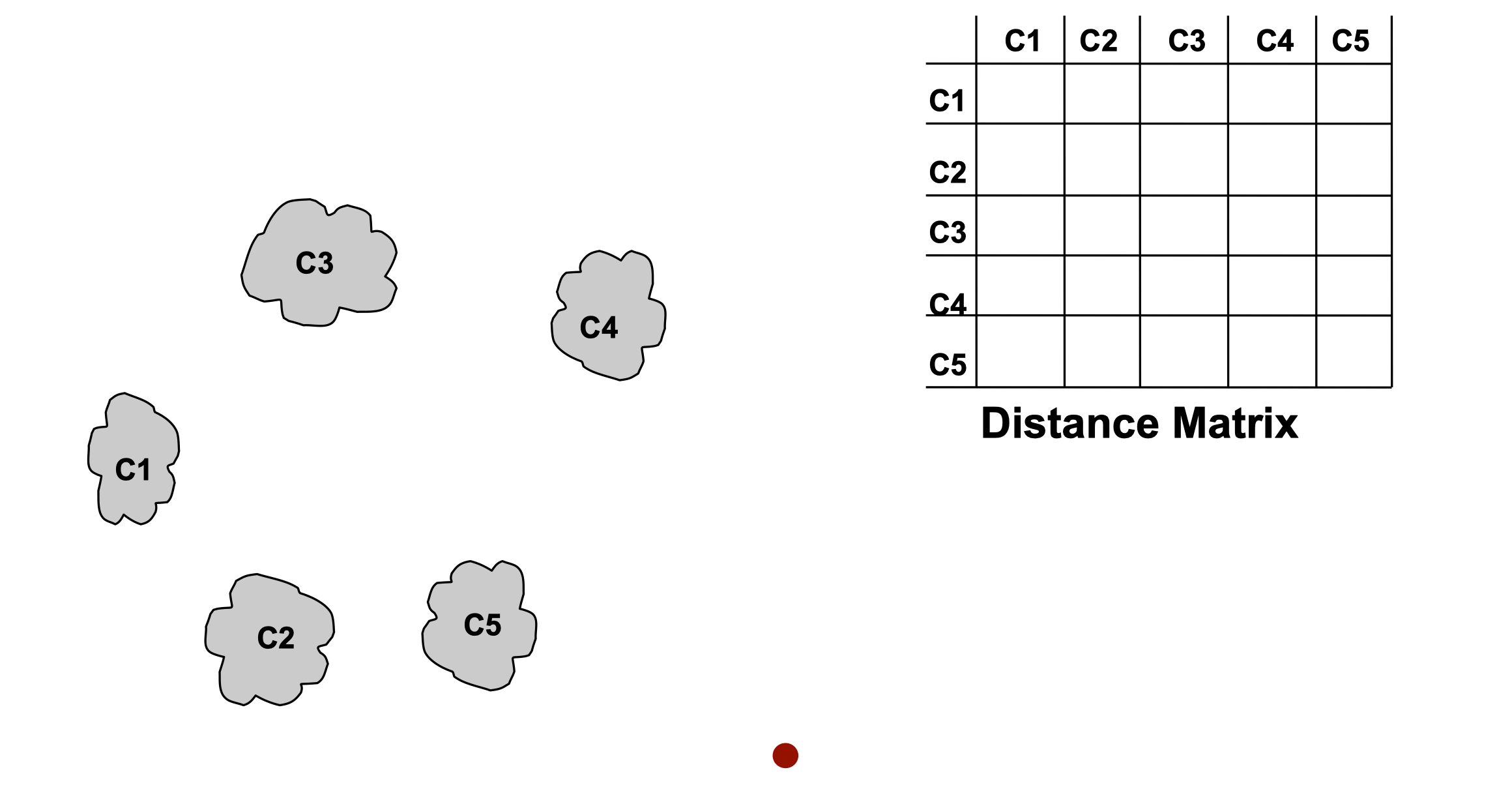
- After some merging steps, we have some clusters
- We want to merge the two closest clusters (C2 and C5) and update the distance matrix
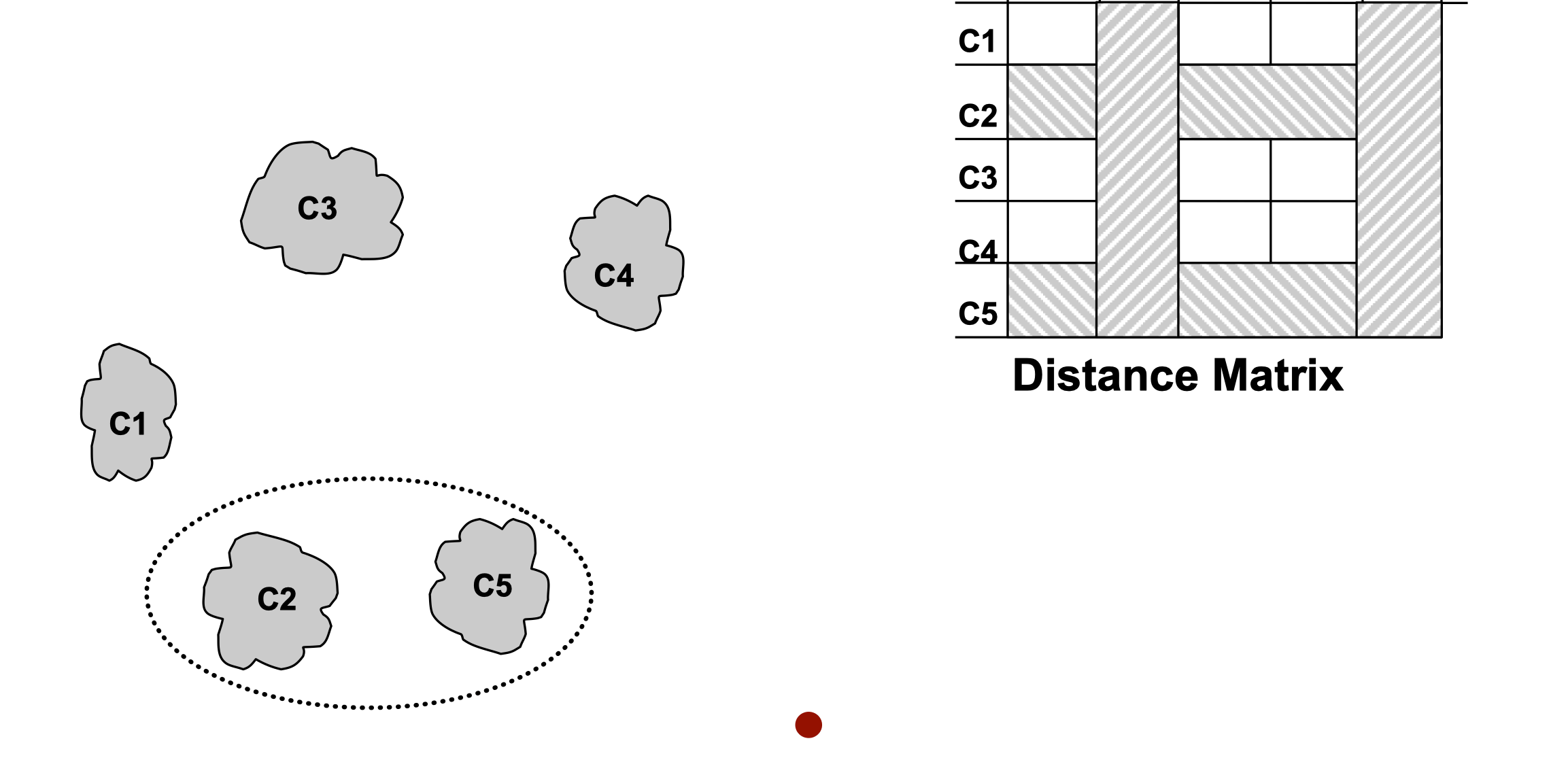
- The question is “How do we update the distance matrix
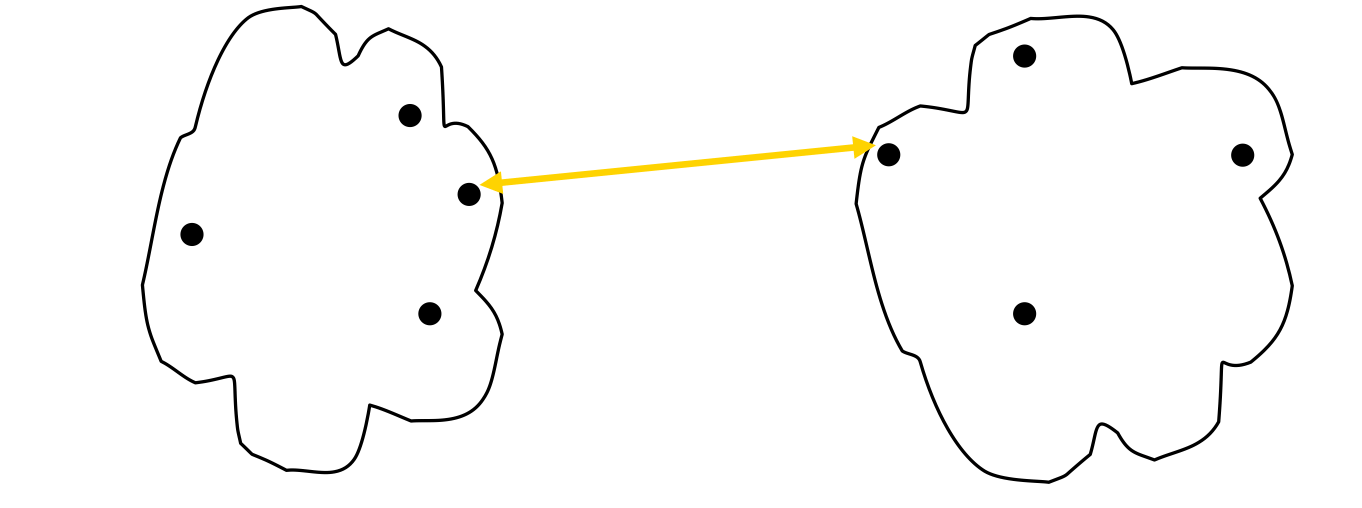
How to Define Inter-Cluster Similarity #
- MIN
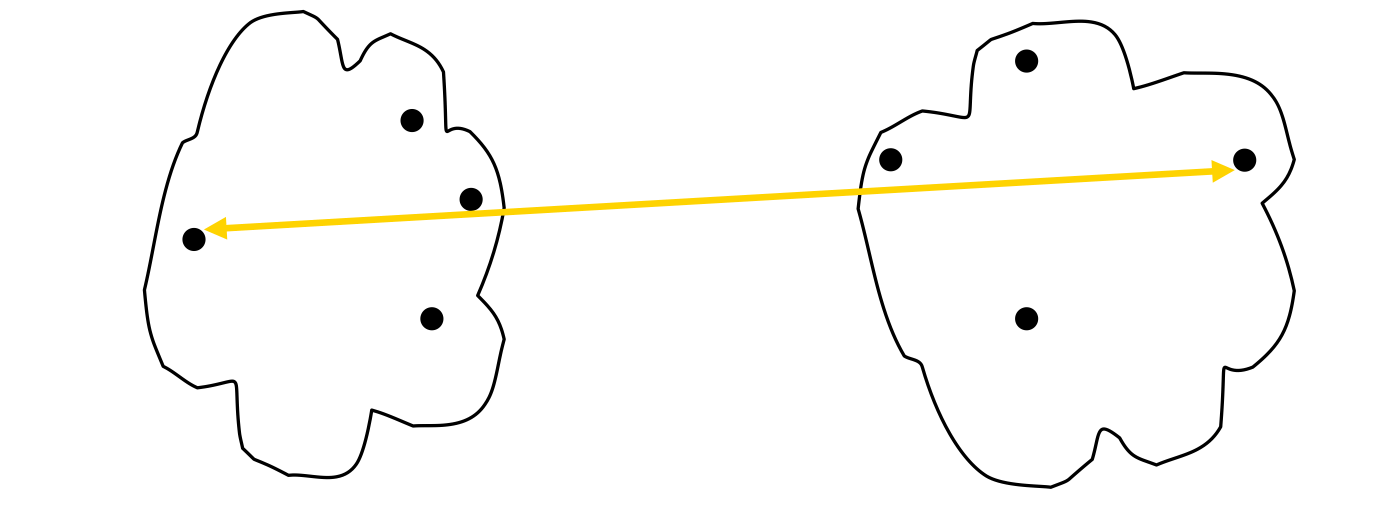
- MAX
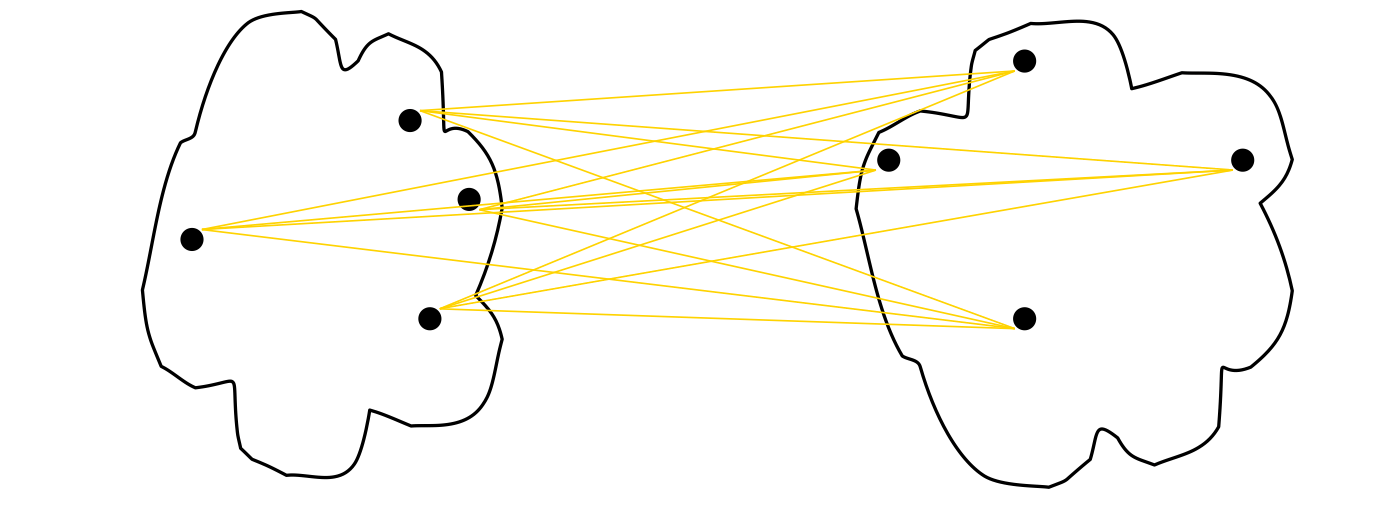
- Group Average
- Distance Between Centroids

- Other methods driven by an objective function
- Ward’s Method uses squared error
Problems and Limitations #
- Once a decision is made to combine two clusters, it cannot be undone
- No objective function is directly minimized
- Different schemes have problems with one or more of the following
- Sensitivity to noise and outliers
- Difficulty handling different sized clusters and convex shapes
- Breaking large clusters
Cluster Validity #
Numerical measures that are applied to judge various aspects of cluster validity, are classified into the following three types
- External Index
- Used to measure the extent to which cluster labels match externally supplied class labels
- Entropy
- Used to measure the extent to which cluster labels match externally supplied class labels
- Internal Index
- Used to measure the goodness of a clustering structure without respect to external information
- Sum of Squared Error (SSE)
- Used to measure the goodness of a clustering structure without respect to external information
- Relative Index
- To compare two different clusterings or clusters
- An external or internal index is used for this function, e.g., SSE or entropy
- To compare two different clusterings or clusters
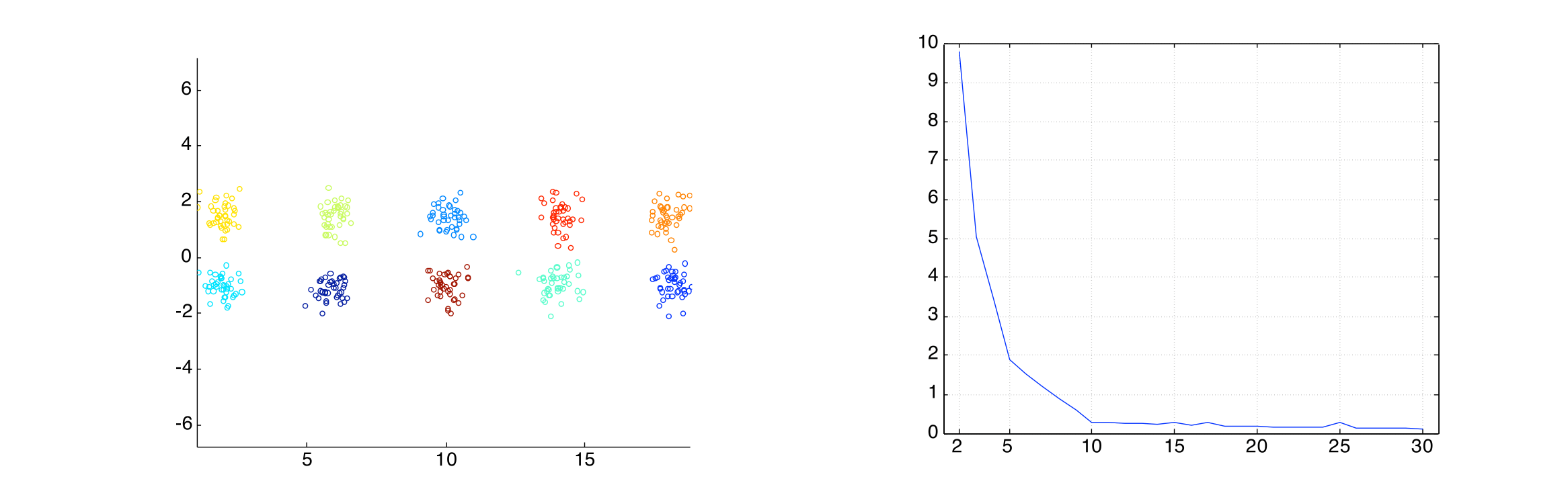
Internal Measures: SSE #
- Clusters in more complicated figures aren’t well separated
- SSE is good for comparing two clusterings or two clusters (average SSE)
- Can also be used to estimate the number of clusters
External Measures of Cluster Validity: Entropy #
- Definition: Entropy
- Entropy measure how uncertain is an event, the larger the entropy the more uncertain is the event

"The validation of clustering structures is the most difficult and frustrating part of cluster analysis. Without a strong effort in this direction, cluster analysis will remain a black art accessible only to those true believers who have experience and great courage."
K-means++ #
- Initialize the centroids as in Algorithm 1
- Run K-means algorithm to improve the clustering

Algorithm Comparison #
- K-means
- No guarantees on the quality of the solution
- It always terminates
- Running time could be exponential but it is OK in practice
- K-means++
- It always terminates
- O(log k)-approximation on the quality of the solution
- In practice the advantage is noticeable for large k