COMP7103 Data Mining #
Topic 2 Association Rules #
Market-Basket Model #
A general many-many mapping (association) between two kinds of things
- A large set of items, e.g., things sold in a supermarket
- A large set of baskets, each of which is a small set of the items, e.g., the things one customer buys on one day
Frequent Itemsets #
Support #
Support for itemset I (s(I)) = the number of baskets containing all items in I
Given a support threshold s, sets of items that appear in at least s baskets are called frequent itemsets

Monotonicity #
For any sets of items I and any set of items J, it holds that

Applications #
- given that many people buy beer and diapers together
- Run a sale on diapers; raise price of beer
- Only useful if many buy diapers & beer
- Items that appear together too often could represent plagiarism
- Unusual words appearing together in a large number of documents
Association Rules #
If-then rules I → j about the contents of baskets, I is a set of items and j is an item
- i → j means
- if a basket contains all the items in I then it is likely to contain j
Confidence #
The probability of j given I
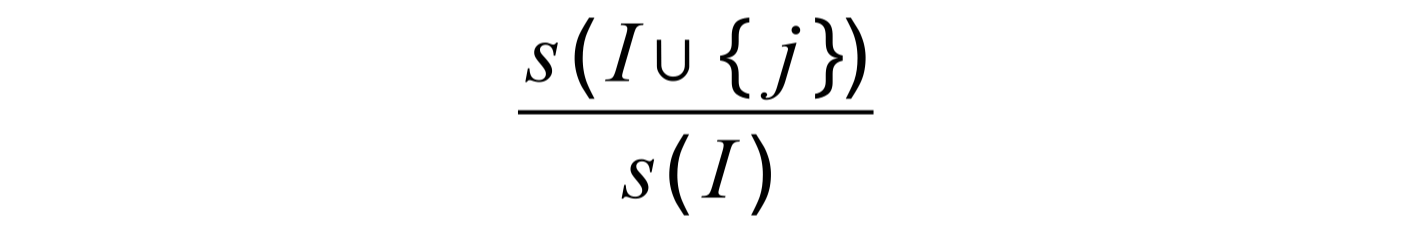

Finding Association Rules #
find all association rules with support ≥ s and confidence ≥ c
Computation Model #
- Data is kept in raw files rather than in a database system
- Stored on disk
- Stored basket-by-basket
- The true cost of mining disk-resident data is usually the number of disk I/O’s
- In practice, association-rule algorithms read data in passes – all baskets read in turn
- we measure the cost by the number of passes an algorithm takes
Association Rules Algorithms #
Naïve Algorithm #
- Read file once, counting in main memory the occurrences of each pair
- From each basket of n items, generate its n (n -1)/2 pairs by two nested loops
- Fails if (#items)^2 exceeds main memory
A-Priori Algorithm #
- A two-pass approach called a-priori limits the need for main memory
- Key idea: monotonicity
- If a set of items appears at least s times, so does every subset
- For pairs: if item i does not appear in s baskets, then no pair including i can appear in s baskets
- Process
- Pass 1
- Read baskets and count in main memory the occurrences of each item (Requires only memory proportional to #items)
- Items that appear at least s times are the frequent items
- Read baskets and count in main memory the occurrences of each item (Requires only memory proportional to #items)
- Pass 2
- Read baskets again and count in main memory only those pairs both of which were found in pass 1 to be frequent
- To count number of item pairs use a hash function
- Requires memory proportional to square of frequent items only, plus a list of the frequent items, plus space for hashing
- Read baskets again and count in main memory only those pairs both of which were found in pass 1 to be frequent
- Pass 1

- One pass for each k
- Needs room in main memory to count each candidate k -set
- For typical market-basket data and reasonable support (e.g., 1%), k = 2 requires the most memory
PCY Algorithm #
- Main observation: during pass 1 of A-priori, most memory is idle
- Use that memory to keep additional info to improve storage during pass 2 of A-priori
- Passes > 2 are the same as in A-Priori
- Process
- Pass 1
- Use a hash function which bucketizes item pairs, that is, maps them to integers in [1,k]
- Each bucket i in [1,k] is associated with a counter ci
- During pass 1, as we examine a basket (e.g. {m,b,d,o})
- update counters of single items
- Generate all item pairs for that basket, hash each of them and add 1 to the corr. counter
- Pass 2
- Count all pairs {i, j } that meet the conditions for being a candidate pair
- Both i and j are frequent items
- The pair {i, j }, hashes to a frequent bucket
- Ignore all pairs belonging to non-frequent buckets (do not use a counter for them)
- Count all pairs {i, j } that meet the conditions for being a candidate pair
- Pass 1
Simple Algorithm #
- Take a random sample of the market baskets
- give a full pass on the data and keep a basket in main memory with probability p
- A random sample is the best representative of a dataset
- Keeping only the first baskets might not contain iPhones for example
- If we cannot have a sample large enough then
- Remove false positives with one more pass
- Run A-priori or one of its improvements in main memory, so you don’t pay for disk I/O each time you give a pass on the data
- Be sure you leave enough space for counts
- Adjust the support threshold s accordingly
SON Algorithm #
- Two passes
- No false positives or false negatives
- Divide the dataset into chunks, where each chunk contains a subset of baskets
- Process
- Pass 1
- Divide the dataset into chunks, where each chunk contains a subset of baskets
- Let pi such that the ith chunk contains a fraction pi of the dataset
- For each chunk i compute all frequent itemsets with support p i x s and store them on disk. This is the set of candidates for next pass
- Pass 2
- Read all frequent itemsets found in the previous pass (candidates)
- For each of them count the number of occurrences and output only those with support at least s
- Pass 1