Database Indexing
Concepts
- Indexing mechanisms used to speed up access to desired data
- Search Key
- An attribute or a set of attributes used to look up records in a file
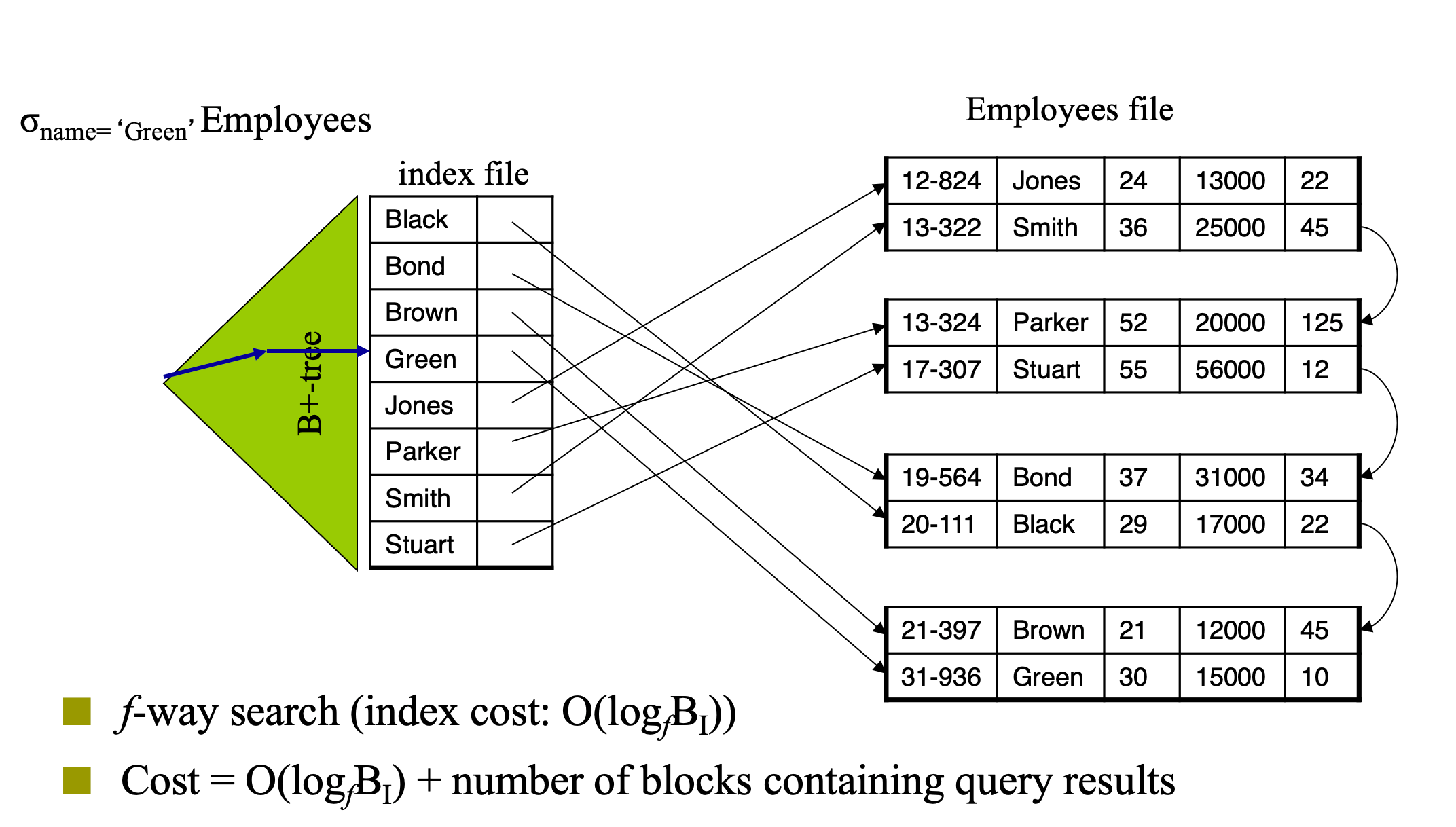
- An index file consists of records (called index entries) of the form
search key - pointer - Index files are typically much smaller than the original file
- Two basic kinds of indices
- Ordered indices: search keys are stored in sorted order
- Hash indices: search keys are distributed across “buckets” using a “hash function”
Good Index
- Index quality is evaluated by several factors
- Access types supported by the index efficiently
- records with a specified value in the attribute (equality query)
- or records with an attribute value falling in a specified range of values (range query)
- Access time – query response time
- Insertion time – data record insertion time
- Deletion time – data record deletion time
- Space overhead – size of the index file
- Access types supported by the index efficiently
Classification of Indexes
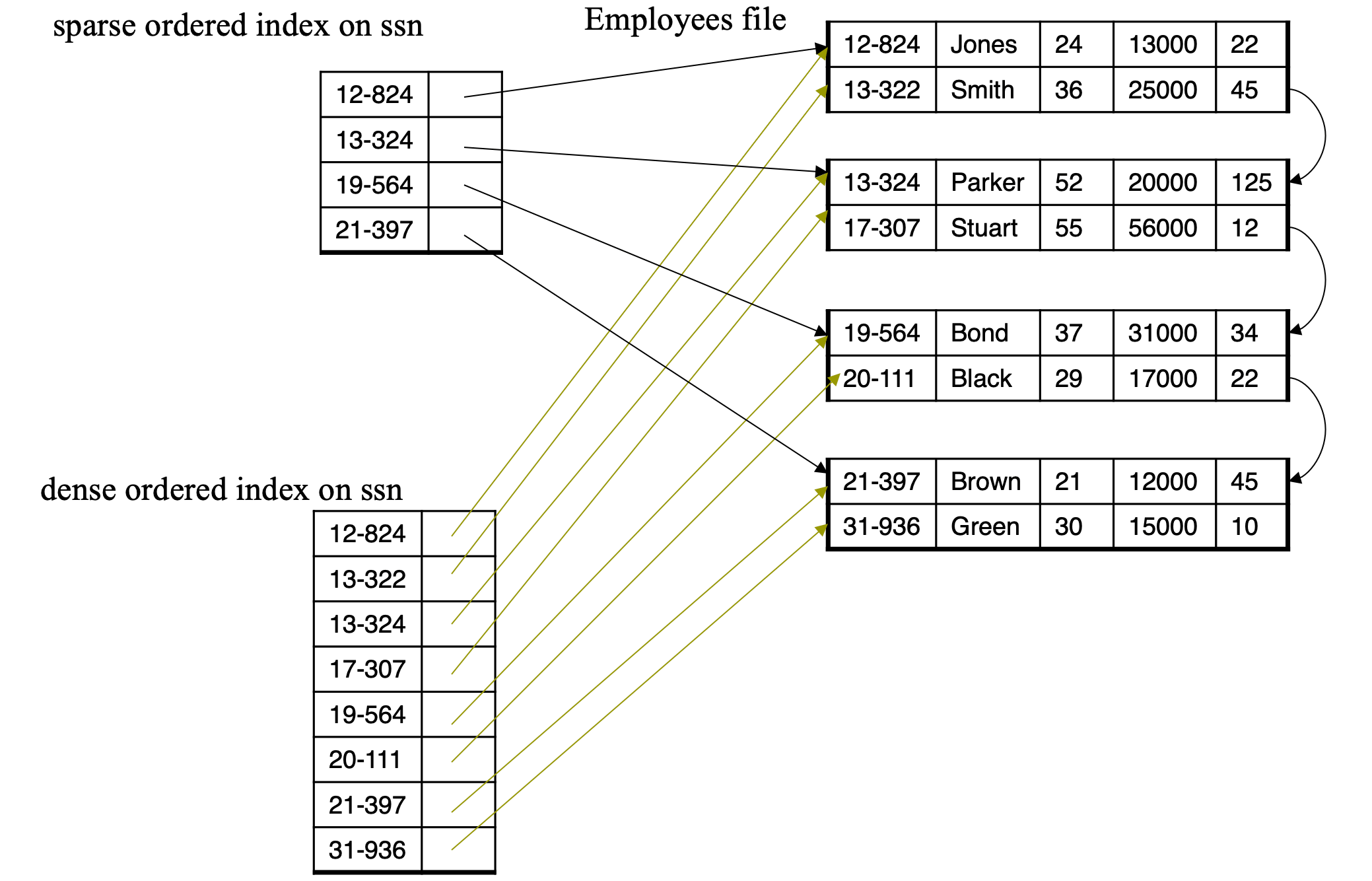
- Primary index
- In a sequentially ordered file, the index whose search key specifies the sequential order of the file
- Secondary index
- an index whose search key specifies an order different from the sequential order of the file
- Also called non-clustered index

- Dense index
- Index record appears for every search-key value in the file
- Sparse Index
- Contains index records for only some search-key values
- Applicable when records are sequentially ordered on search-key
- Less space and less maintenance overhead for insertions and deletions
- Generally slower than dense index for locating records
- Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block
Primary and Secondary Indices
- Secondary indices have to be dense
- Indices offer substantial benefits when searching for records
- Index is much smaller than relation file (cheap scan)
- Index can be ordered (fast search)
- When a file is modified, every index on the file must be updated
- Updating indices imposes overhead on database modification
- Indexes should be used with care
- Sequential scan using primary index is efficient, but a sequential scan using a secondary index is expensive
- Each record access may fetch a new block from disk
Multilevel Index
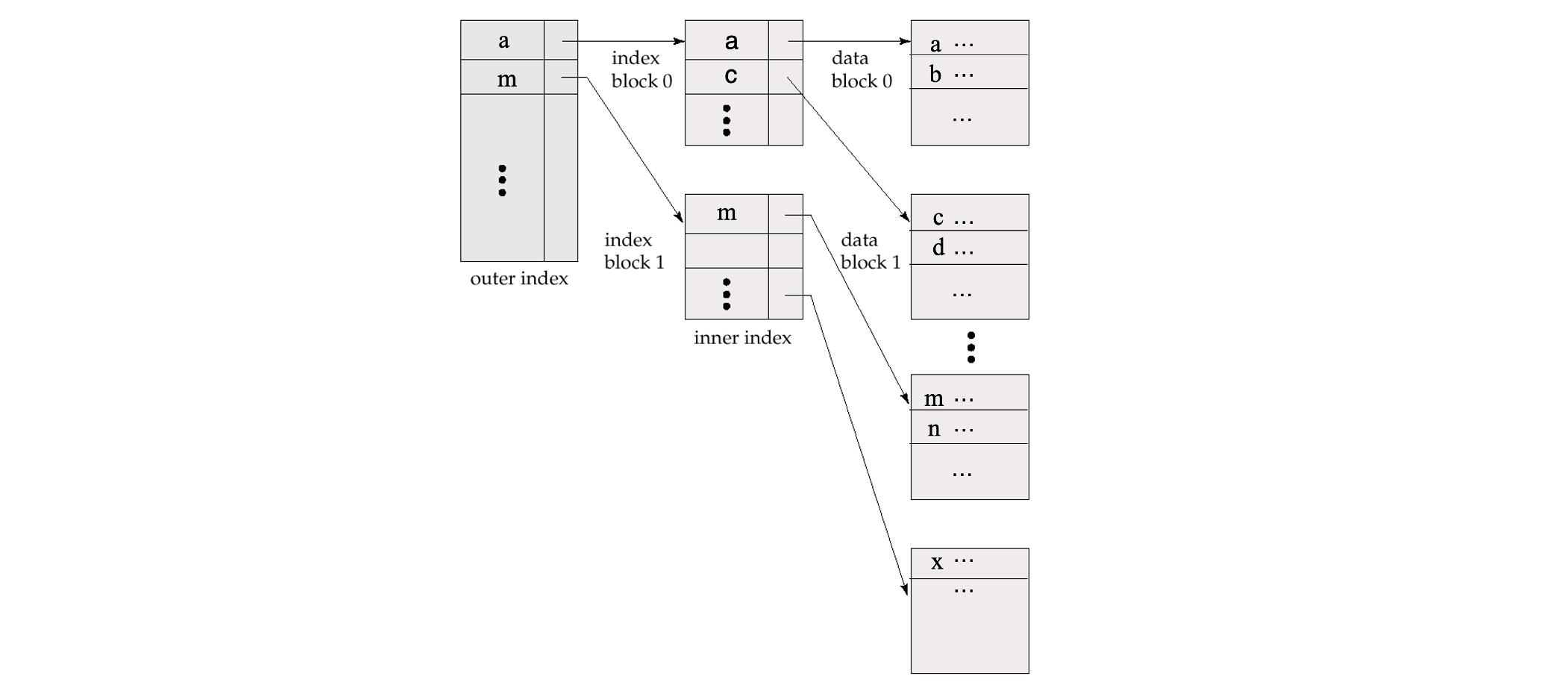
- If index does not fit in memory, access becomes expensive
- To reduce number of disk accesses to index records, treat 1st level of index kept on disk as a sequential file and construct a sparse index on it
- outer index – a sparse index on 1st-level index file
- inner index – the 1st-level index file
- If even outer index is too large to fit in main memory, yet another level of index can be created, and so on
B+-Tree Index Files
- A dynamic, multi-level index
- Advantage
- automatically reorganizes itself with small local changes, in the face of insertions and deletions
- Reorganization of entire file is not required to maintain performance
- Disadvantage of B+-trees
- Extra insertion and deletion overhead, space overhead
- Advantages of B+-trees outweigh disadvantages, and they are used extensively
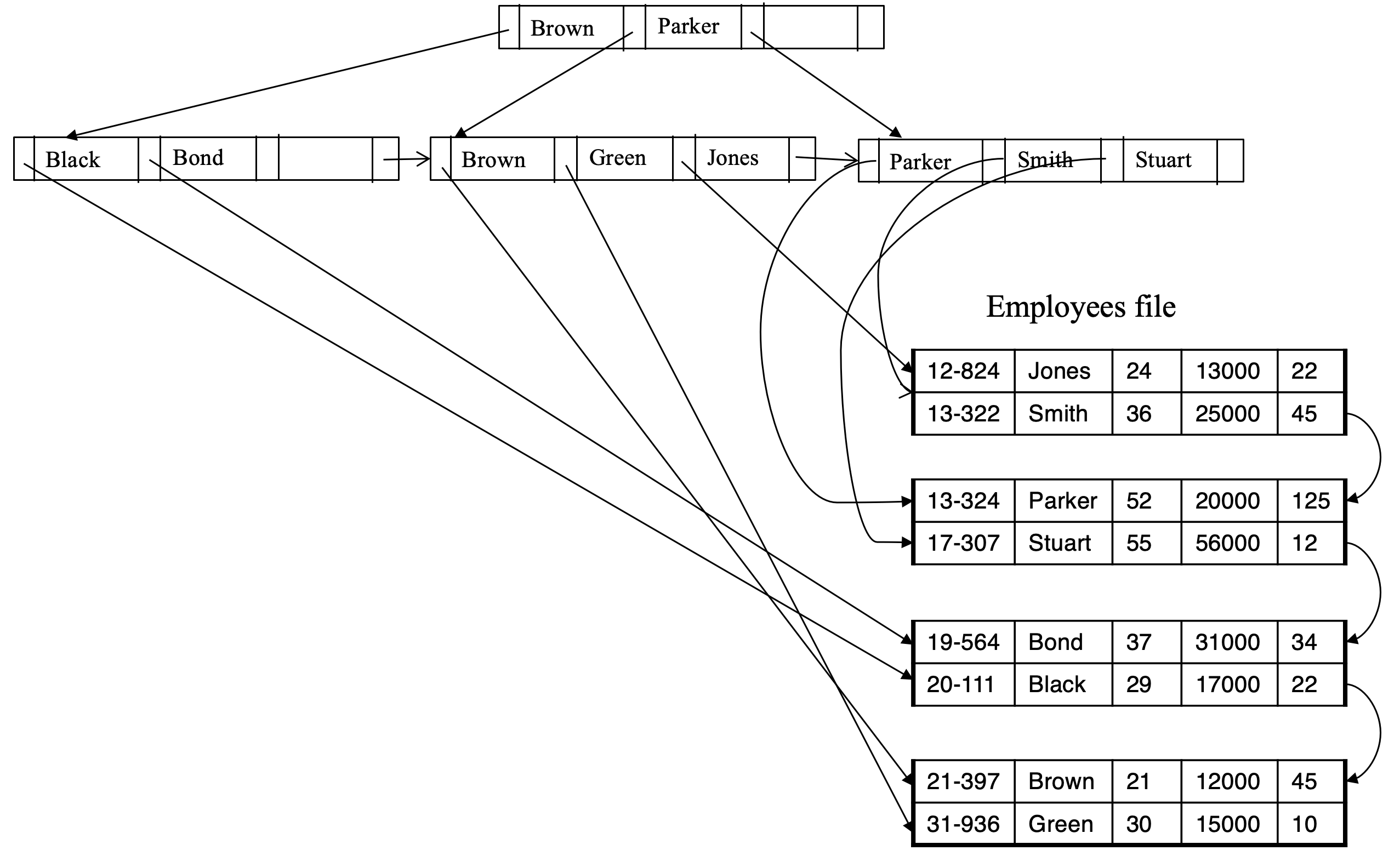
Basic Properties
- Disk-based tree structure
- every node of the tree is a block and has an address (block-id) on the disk
- Multiway tree
- each node has multiple children (between n/2 and n, where n/2 is the order or degree of the tree)
- Therefore, at least 50% of the space in a node is guaranteed to be occupied (this rule may not apply to tree root)
- Balanced tree
- all paths from the root to a leaf have the same length
- guarantees good search performance (to be seen later)
- Disjoint partition of attribute domain into ranges
- each sub-tree indexes a range in the attribute domain
- the entries of a directory node define the separators between domain intervals
- leaf nodes store index entries and pointers to the relation file
Non-Leaf Nodes in B+-Trees
- Each non-leaf node contains up to n-1 search key values and up to n pointers
- All non-leaf nodes (except root) contain at least n/2 pointers (n/2 is sometimes called the minimum fan-out or degree)
- Non leaf nodes form a multi-level sparse index on the leaf nodes. For a non-leaf node with m pointers
- All the search-keys in the subtree to which P1 points are less than K1
- For 2 <= i <= n – 1, all the search-keys in the subtree to which Pi points have values greater than or equal to Ki–1 and smaller than Km–1

Leaf Node in a B+-Tree
- Contains between (n-1)/2 and n-1 entries
- Each index entry is a search key value + a record-id
- If Li, Lj are leaf nodes and i < j, Li’s search-key values are all smaller than Lj’s search-key values
- Each leaf node is linked with a pointer to the next node
Observations
- Since the inter-node connections are done by pointers, “logically” close blocks need not be “physically” close
- Nodes of the tree are dynamically created/deleted, so we cannot guarantee physical closeness
- The non-leaf levels of the B+-tree form a hierarchy of sparse indices
- The B+-tree contains a relatively small number of levels (logarithmic in the size of the main file), thus searches can be conducted efficiently
- Insertions and deletions to the main file can be handled efficiently (in logarithmic time)
Queries
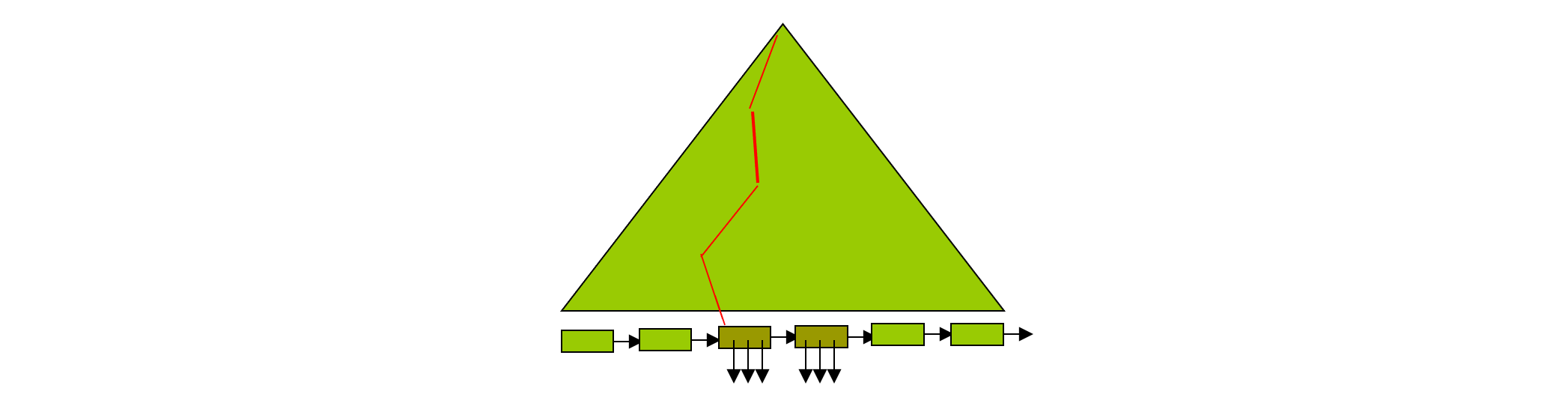
Find all records with a search-key value of k
- Start with the root node
- Examine the node for the smallest search-key value > k
- If such a value exists, assume it is Ki. Then follow Pi to the child node. (E.g. P2 is for keys in K1 <= Keys < K2 )
- Otherwise k >= Kn–1, where there are n pointers in the node. Then follow Pn to the child node
- If the node reached by following the pointer above is not a leaf node, repeat the above procedure on the node, and follow the corresponding pointer
- Eventually reach a leaf node. If for some i, key Ki = k follow pointer Pi to the desired record. Else no record with search-key value k exists
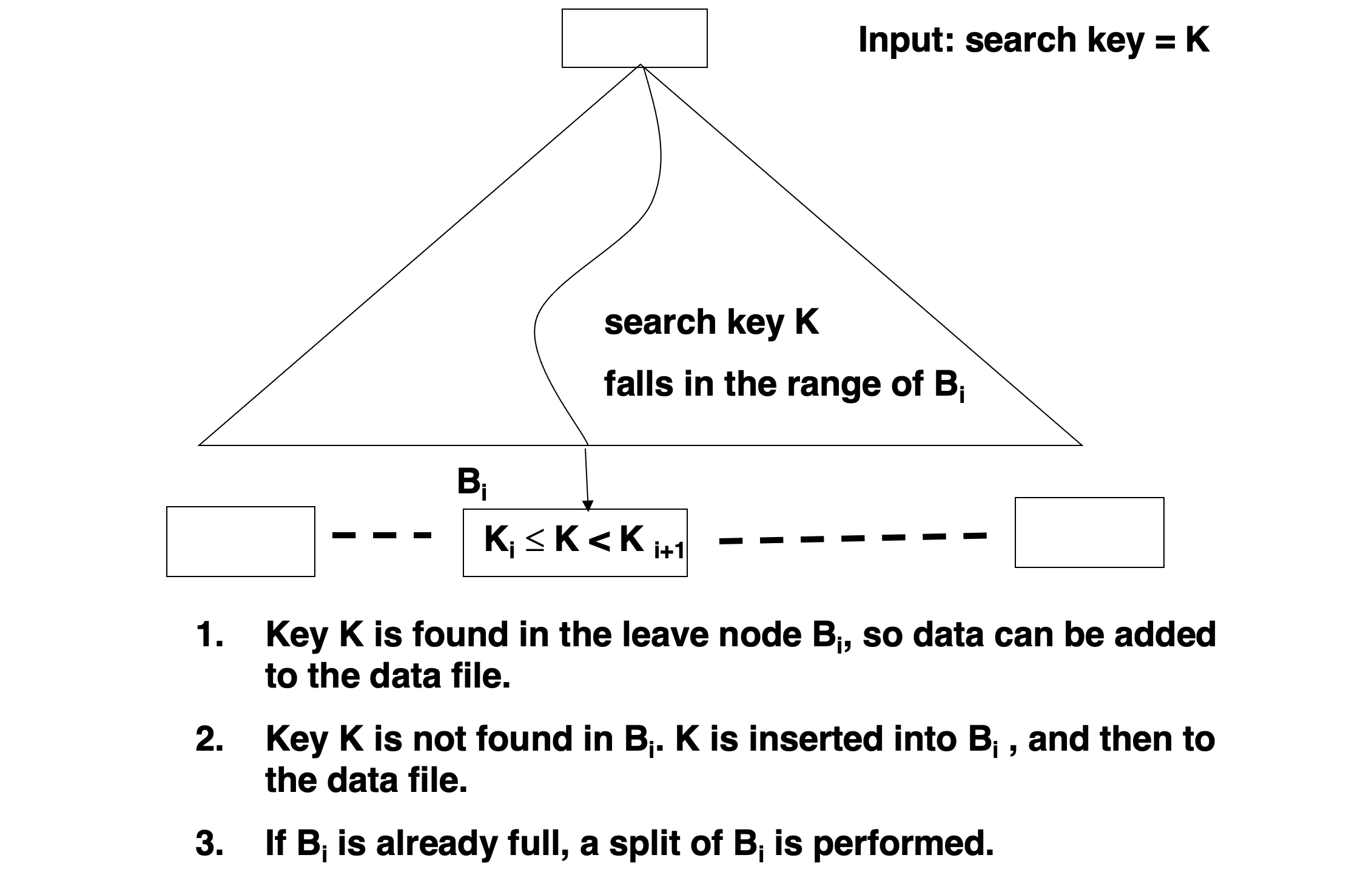
- Start with the root node
In processing a query, a path is traversed in the tree from the root to some leaf node
If there are K search-key values in the file, the path is not longer than log(n/2)(K). (The degree of a node is no less than n/2)
A node has generally the same size of a disk block, typically 4 kilobytes, and n is typically around 100 (40 bytes per index entry)
With 1 million search key values and n/2 = 50, at most log50(1,000,000) = 4 nodes are accessed in a lookup
Contrast this with a balanced binary tree with 1 million search key values — around 20 nodes are accessed in a lookup
- (log2(1,000,000) ~= 20)
- above difference is significant since every node access may need a disk I/O, costing around 10 milliseconds!
Similar result for a binary search of an ordered sequential file
Range Queries
- Find all records with a search-key value between k and m (k<m)
- Start with the root node
- Examine the node for the smallest search-key value > k
- If such a value exists, assume it is Kj
- Then follow Pi to the child node
- Otherwise k >= Kn–1, where there are n pointers in the node
- Then follow Pn to the child node.
- If the node reached by following the pointer above is not a leaf node, repeat the above procedure on the node, and follow the corresponding pointer
- Eventually reach a leaf node. If for some i, k <= Ki <= m follow pointer Pi to the desired record. Continue with next entry Ki+1, while Ki+1 <= m. If at end of leaf node follow pointer to next node, until Ki >m or end of index
- Start with the root node
Insertion
- Find the leaf node in which the search-key value to be inserted would appear
- If the search-key value is already there in the leaf node, record is added to file and if necessary one more pointer is associated with the search key value
- If the search-key value is not there, then add the record to the main file. Then
- If there is room in the leaf node, insert (key-value, pointer) pair in the leaf node
- Otherwise, split the node (along with the new (key-value, pointer) entry) as discussed in the next slides
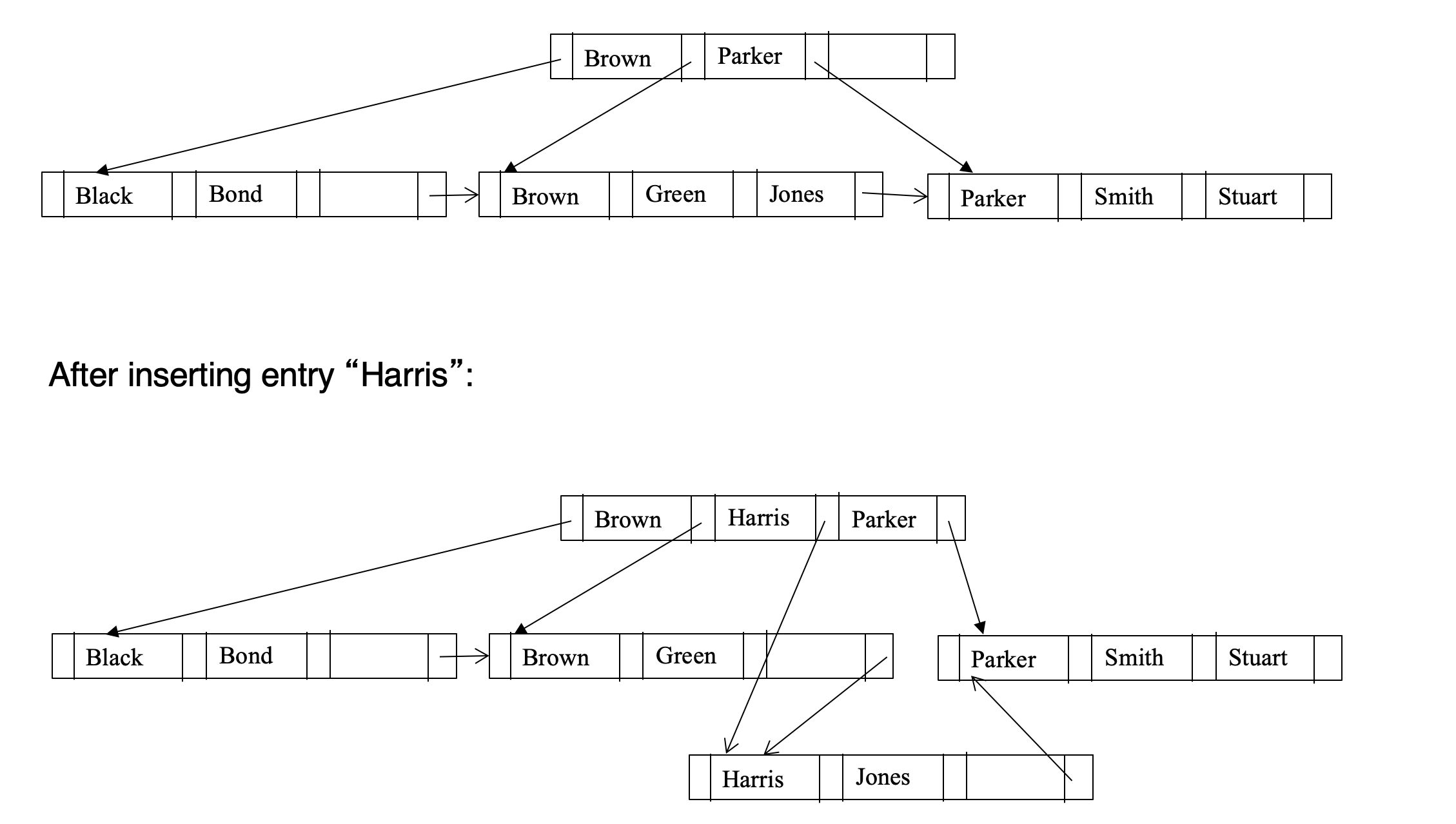
Splitting
- Splitting a node
- take the (search-key value, pointer) pairs (including the one being inserted) in sorted order. Place the first n/2 in the original node, and the rest in a new node
- let the new node be p, and let k be the least key value in p. Insert (k,p) in the parent of the node being split. If the parent is full, split it and propagate the split further up
- The splitting of nodes proceeds upwards till a node that is not full is found. In the worst case the root node may be split increasing the height of the tree by 1
- Non-leaf node splitting
- Overflown node has n+1 pointers and n values
- Leave first n/2 key values and n/2+1 pointers to original node
- Move last n/2 key values and n/2+1 pointers to new node
- insert (middle key value, pointer to new node) to parent node
Deletion
- Find the record to be deleted, and remove it from the relation file
- Remove (search-key value, record-id) of deleted record from the leaf node of the B+-tree
- If the node has too few entries due to the removal, and the entries in the node and a sibling fit into a single node, then
- Insert all the search-key values in the two nodes into a single node (the one on the left), and delete the other node. (Deletion triggers a merge)
- Delete the pair (Ki–1, Pi), where Pi is the pointer to the deleted node, from its parent, recursively using the above procedure
- Otherwise, if the node has too few entries due to the removal, and the entries in the node and a sibling does not fit into a single node, then
- Redistribute the pointers between the node and a sibling such that both have more than the minimum number of entries. (Deletion and rebalancing)
- Update the corresponding search-key value in the parent of the node
- The node deletions may cascade upwards until a node which has n/2 or more pointers is found. If the root node has only one pointer after deletion, it is deleted and the sole child becomes the root

Static Hashing
- A bucket is a unit of storage containing one or more records (a bucket is typically a disk block)
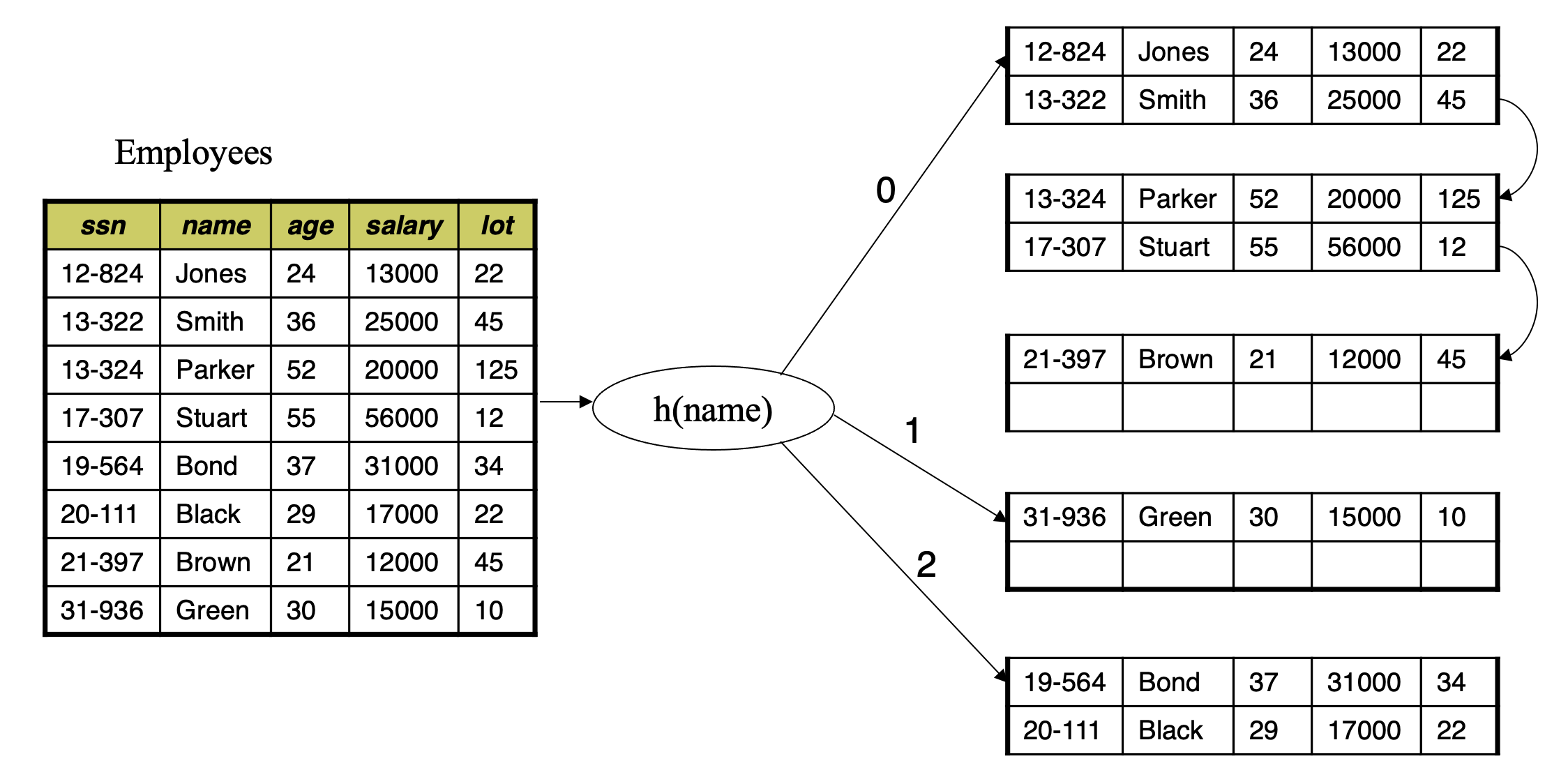
- In a hash file organization we obtain the bucket of a record directly from its search-key value using a hash function
- Hash function h is a function from the set of all search-key values K to the set of all bucket addresses B
- Hash function is used to locate records for access, insertion as well as deletion
- Records with different search-key values may be mapped to the same bucket; thus entire bucket has to be searched sequentially to locate a record. (Collision)
Hash Function
- Worst case has function maps all search-key values to the same bucket; this makes access time proportional to the number of search-key values in the file
- An ideal hash function is uniform, i.e., each bucket is assigned the same number of search-key values from the set of all possible values
- Ideal hash function is random, so each bucket will have the same number of records assigned to it irrespective of the actual distribution of search-key values in the file
- Typical hash functions perform computation on the internal binary representation of the search-key
- For example, for a string search-key, the binary representations of all the characters in the string could be added and the sum modulo the number of buckets could be returned
Handling of Bucket Overflows
- Bucket overflow can occur because of
- Insufficient buckets
- Skew in distribution of records. This can occur due to two reasons
- multiple records have same search-key value
- chosen hash function produces non-uniform distribution of key values
- Although the probability of bucket overflow can be reduced, it cannot be eliminated; it is handled by using overflow buckets
- Overflow chaining / closed hashing – the overflow buckets of a given bucket are chained together in a linked list
Hash Indices
- Hashing can be used not only for file organization, but also for index-structure creation
- A hash index organizes the search keys, with their associated record pointers, into a hash file structure
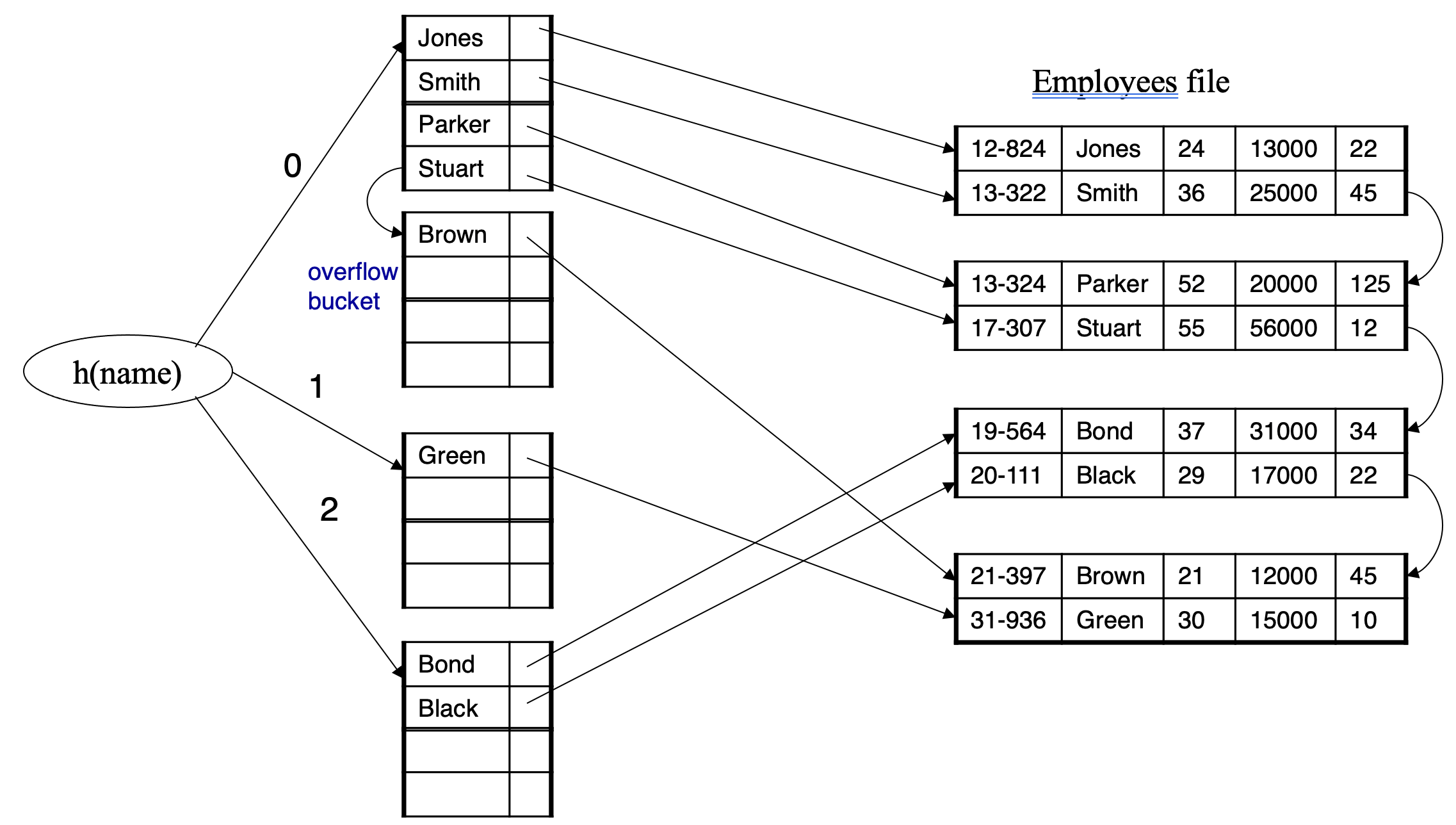
Deficiencies of Static Hashing
- In static hashing, function h maps search-key values to a fixed set of B of bucket addresses
- Databases grow with time. If initial number of buckets is too small, performance will degrade due to too much overflows
- If file size at some point in the future is anticipated and number of buckets allocated accordingly, significant amount of space will be wasted initially
- If database shrinks, again space will be wasted
- One option is periodic re-organization of the file with a new hash function, but it is very expensive.
- These problems can be avoided by using techniques that allow the number of buckets to be modified dynamically (dynamic hashing)
